题目内容
4.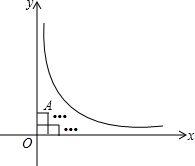 如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.
如图,在曲线y=$\frac{3}{x}$(x>0)与两坐标轴之间的区域A内,最多可以水平排放边长为$\frac{1}{2}$的正方形35个.
分析 把x=$\frac{1}{2}$和y=$\frac{1}{2}$分别代入函数解析式求得相应的y、x的值.即可得到该区域内所摆放的正方形的列、行数.
解答 解:当x=$\frac{1}{2}$时,y=6,则$\frac{6}{\frac{1}{2}}$=12(个).
当x=1时,y=3,则$\frac{3}{\frac{1}{2}}$=6(个).
当x=$\frac{3}{2}$时,y=2,则$\frac{2}{\frac{1}{2}}$=4(个).
当x=2时,y=$\frac{3}{2}$,则$\frac{\frac{3}{2}}{\frac{1}{2}}$=3(个).
当x=$\frac{5}{2}$时,y=$\frac{6}{5}$,则$\frac{\frac{6}{5}}{\frac{1}{2}}$=$\frac{12}{5}$,能摆放2个.
当x=3时,y=1,则$\frac{1}{\frac{1}{2}}$=2(个).
当x=$\frac{7}{2}$时,y=$\frac{6}{7}$,则$\frac{\frac{6}{7}}{\frac{1}{2}}$=$\frac{12}{7}$,能摆放1个.
当x=4时,y=$\frac{3}{4}$,则$\frac{\frac{3}{4}}{\frac{1}{2}}$=$\frac{3}{2}$,能摆放1个.
当x=$\frac{9}{2}$时,y=$\frac{2}{3}$,则$\frac{\frac{2}{3}}{\frac{1}{2}}$=$\frac{4}{3}$,能摆放1个.
当x=5时,y=$\frac{3}{5}$,则$\frac{\frac{3}{5}}{\frac{1}{2}}$=$\frac{6}{5}$,能摆放1个.
当x=$\frac{11}{2}$时,y=$\frac{6}{11}$,则$\frac{\frac{6}{11}}{\frac{1}{2}}$=$\frac{12}{11}$,能摆放1个.
当x=6时,y=$\frac{1}{2}$,能摆放1个.
所以,12+6+4+3+2++2+1+1+1+1+1+1=35(个).
故答案是:35.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 调查中学生最喜爱的电视节目 | B. | 调查某张试卷上的印刷错误 | ||
| C. | 调查某厂家生产的电池的使用寿命 | D. | 调查中学生上网情况 |
| 年数n | 高度h(厘米) |
| 第1年 | 100 |
| 第2年 | 100+5 |
| 第3年 | 100+10 |
| 第4年 | 100+15 |
(2)求第几年时,树苗高度为130厘米.
 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{BG}$=$\frac{1}{4}$,则$\frac{AD}{AB}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |

| A. | 4月份商场的商品销售总额是75万元 | |
| B. | 1月份商场服装部的销售额是22万元 | |
| C. | 5月份商场服装部的销售额比4月份减少了 | |
| D. | 3月份商场服装部的销售额比2月份减少了 |

 如图,直线y=-x+m交x轴于点A、交y轴于点B,与双曲线y=$\frac{k}{x}$在第一象限交于C、D两点,若AC•BC=6,则k=3.
如图,直线y=-x+m交x轴于点A、交y轴于点B,与双曲线y=$\frac{k}{x}$在第一象限交于C、D两点,若AC•BC=6,则k=3.