题目内容
4. 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
分析 根据相似三角形的性质,可得PC的长,根据正切函数等于对边比邻边,可得答案.
解答 解:如图: ,
,
CM═$\frac{1}{2}$DM=1,HN=2NE=2.
△PCM∽△PHN,
$\frac{PC}{PH}$=$\frac{MC}{NH}$=$\frac{1}{2}$,
PC=$\frac{1}{2}$(PC+CH),
解得PC=3
PH=6.
tan∠NPH=$\frac{NH}{PH}$=$\frac{2}{6}$=$\frac{1}{3}$,
故选:C.
点评 本题考查了锐角三角函数的定义,利用相似三角形的性质得出PC的值是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
12.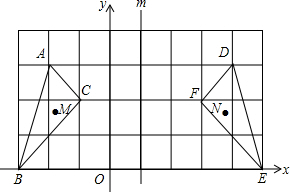 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
 如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )
如图,在平面直角坐标系中,△ABC与△DEF关于直线m=1对称,点M、N分别是这两个三角形中的对应点,如果点M的横坐标是a,那么点N的横坐标是( )| A. | -a | B. | -a+1 | C. | a+2 | D. | -a+2 |
13.记S(n)为非负整数n的各个数位上的数字之和,如S(0)=0,S(1)=1,S(1995)=1+9+9+5=24.则S(1)+S(2)+S(3)+…+S(2015)=( )
| A. | 28097 | B. | 28098 | C. | 28077 | D. | 28087 |
14.下列函数不是一次函数的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=-$\frac{1}{3}$x | C. | y=$\frac{x}{π}$-1 | D. | y=2x+b |
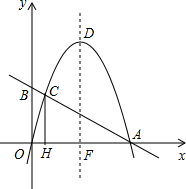 如图,二次函数y=-x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足H,设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.
如图,二次函数y=-x2+bx的图象与x轴的正半轴交于点A(4,0),过A点的直线与y轴的正半轴交于点B,与二次函数的图象交于另一点C,过点C作CH⊥x轴,垂足H,设二次函数图象的顶点为D,其对称轴与直线AB及x轴分别交于点E和点F.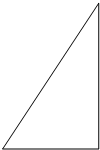 现有一块直角三角形边角料,两条直角边分别长6cm和8cm,要你利用这块边角料裁剪出一个面积最大的正方形材料,你准备怎样裁剪?所得正方形的面积是多少?注意:要讨论哦,自己标上字母.
现有一块直角三角形边角料,两条直角边分别长6cm和8cm,要你利用这块边角料裁剪出一个面积最大的正方形材料,你准备怎样裁剪?所得正方形的面积是多少?注意:要讨论哦,自己标上字母.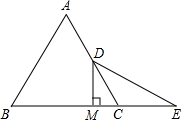 如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.
如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.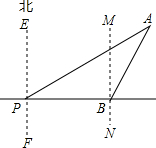 如图,一艘轮船位于P时测得,灯塔A在其北偏东60°方向,当它沿着正东方向行驶400海里到达B处,此时测得灯塔A在北偏东30°方向,已知以灯塔A为圆心,350海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁危险?$(\sqrt{3}≈1.7)$.
如图,一艘轮船位于P时测得,灯塔A在其北偏东60°方向,当它沿着正东方向行驶400海里到达B处,此时测得灯塔A在北偏东30°方向,已知以灯塔A为圆心,350海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁危险?$(\sqrt{3}≈1.7)$.