题目内容
9.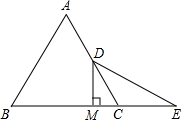 如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.
如图,△ABC是等边三角形,点E是BC延长线上的点,BE的垂直平分线交AC于点D,垂足为M,CE=CD,求证:AD=CD.
分析 先根据△ABC是等边三角形可知∠B=∠ACB=60°,再根据CE=CD可知∠CDE=∠E,由三角形外角的性质可知∠ACB=∠E+∠CDE=60°,故∠E=30°,由DE垂直平分BE可得出∠E=∠DBE=30°,故BD=DE,再根据等边三角形的三线合一性质得出AD=CD.
解答 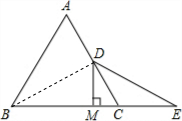 证明:连接BD,
证明:连接BD,
∵△ABC是正三角形,
∴∠B=∠ACB=60°,
∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB是△CDE的外角,
∴∠ACB=∠E+∠CDE,
∴∠E=30°,
又∵DM垂直平分BE,
∴BD=DE,
∴∠E=∠DBC=30°,
∵∠B=60°,
∴∠ABD=∠DBC=30°,即BD是正△ABC的角平分线,
∴BD又是边AC的中线,即D点是AC边的中点,
∴AD=CD.
点评 本题考查的是等边三角形的性质及三角形外角的性质,根据题意得出△BDE是等腰三角形是解答此题的关键.

练习册系列答案
相关题目
4. 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )
 如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )
如图,正方体的棱长为3,点M,N分别在CD,HE上,CM=$\frac{1}{2}$DM,HN=2NE,HC与NM的延长线交于点P,则tan∠NPH的值为( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
18. 关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
 关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )
关于x的一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集是( )| A. | x<-3 | B. | x≤-3 | C. | x<-1 | D. | x≤-1 |
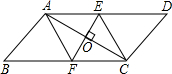 已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.
已知:如图,在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.求证:四边形AFCE是菱形.