题目内容
3.∠α与它的余角相等,∠β与它的补角相等,则∠α+∠β=135°.分析 根据余角、补角的定义求得∠α,∠β的度数,再相加计算即可求解.
解答 解:∵∠α与它的余角相等,∠β与它的补角相等,
∴∠α=45°,∠β=90°,
∴∠α+∠β=45°+90°=135°.
故答案为:135.
点评 本题考查补角、余角的定义:如果两个角的和为180°,则这两个角互为补角,如果两个角的和为90°,则这两个角互为余角.

练习册系列答案
相关题目
14.要组织一次排球邀请赛,参赛的每两个队之间比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
| A. | $\frac{1}{2}$x(x+1)=28 | B. | x(x-1)=28 | C. | x(x+1)=28 | D. | $\frac{1}{2}$x(x-1)=28 |
11.方程x(x-1)=0的解是( )
| A. | x=1 | B. | x1=0,x2=1 | C. | x=0 | D. | x1=0,x2=-1 |
15.若点P(a,4-a)是第二象限的点,则a必须满足( )
| A. | a<0 | B. | a<4 | C. | 0<a<4 | D. | a>4 |
12.目前我国已建立了比较完善的经济困难学生资助体系,某校去年上半年发放给每个经济困难学生389元,今年上半年发放了438元,设每半年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是( )
| A. | 438(1+x)2=389 | B. | 389(1+x)2=438 | C. | 389(1+2x)=438 | D. | 438(1+2x)=389 |
13.下列方程中,一定是关于x的一元二次方程的是( )
| A. | (k2+1)x2-4=0 | B. | ax2+bx+c=0 | C. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-3=0 | D. | (x+4)(x-2)=x2 |
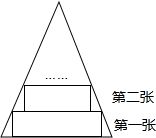 如图所示,一张等腰三角形纸片,底边长为18cm,底边上的高为18cm,现沿底边依次由下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是第5张.
如图所示,一张等腰三角形纸片,底边长为18cm,底边上的高为18cm,现沿底边依次由下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是第5张.