题目内容
将长方形ABCD沿AE折叠，得到如图所示的图形．如果∠CED′=50°，那么∠EAD′=________．
25°
分析：由折叠的性质可知∠DEA=∠D′EA，而∠DED′=180°-∠CED′=130°，由此可求∠D′EA，在Rt△AD′E中，利用互余关系可求∠EAD′．
解答：由折叠的性质可知∠DEA=∠D′EA，
∵∠DED′=180°-∠CED′=130°，∠DED′=∠DEA+∠D′EA，
∴∠D′EA=65°，
在Rt△AD′E中，∠EAD′=90°-∠D′EA=25°．
故本题答案为：25°．
点评：本题考查了折叠的性质．关键是由邻补角的性质及折叠的两个角相等求解．
分析：由折叠的性质可知∠DEA=∠D′EA，而∠DED′=180°-∠CED′=130°，由此可求∠D′EA，在Rt△AD′E中，利用互余关系可求∠EAD′．
解答：由折叠的性质可知∠DEA=∠D′EA，
∵∠DED′=180°-∠CED′=130°，∠DED′=∠DEA+∠D′EA，
∴∠D′EA=65°，
在Rt△AD′E中，∠EAD′=90°-∠D′EA=25°．
故本题答案为：25°．
点评：本题考查了折叠的性质．关键是由邻补角的性质及折叠的两个角相等求解．
练习册系列答案
相关题目
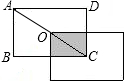如图所示，将长方形ABCD沿对角线的方向平移，且平移后的图形的一个顶点恰好落在AC的中点O处，则移动前后两个图形重叠部分的面积为原长方形面积的
16、将长方形ABCD沿AE折叠，得到如图所示的图形．如果∠CED′=50°，那么∠EAD′=
如图，将长方形ABCD沿AE折叠，若∠BAD′比∠D′AE大16°，则∠D′AE=
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F处，如果∠BAF=60度，那么∠DAE=（ ）
如图，将长方形ABCD沿AE折叠，使点D落在BC边上的点F，若∠DAE=15°，则∠BAF=（ ）