Question

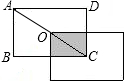如图所示，将长方形ABCD沿对角线的方向平移，且平移后的图形的一个顶点恰好落在AC的中点O处，则移动前后两个图形重叠部分的面积为原长方形面积的

 

．

Answer 1

分析：结合图形，由平移的性质，根据已知条件，可知A与O重合．根据三角形的中位线定理，重叠部分长方形的长和宽分别为原长方形的长和宽的一半，所以移动前后两个图形重叠部分的面积为原长方形面积的

1

4

．

解答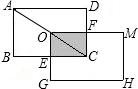：解：如图．
∵将长方形ABCD沿对角线的方向平移，且平移后的图形的一个顶点恰好落在AC的中点O处，
∴A与O重合，OA=OC，OG∥AB，OM∥AD，
∴CE=

1

2

BC，CF=

1

2

CD．
∴重叠部分的面积=长方形OECF的面积=CE•CF=

1

2

BC•

1

2

CD=

1

4

BC•CD=

1

4

×长方形ABCD的面积．
故答案为

1

4

．

点评：本题综合考查了平移的性质和三角形中位线定理．平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．