题目内容
如图1,抛物线 与
与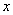 轴交于
轴交于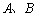 两点,与
两点,与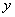 轴交于点
轴交于点 ,连结AC,若
,连结AC,若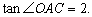
(1)求抛物线的解析式;
(2)抛物线对称 轴上有一动点P,当
轴上有一动点P,当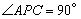 时,求出点
时,求出点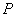 的坐标;
的坐标;
(3)如图2所示,连结 ,
, 是线段
是线段 上(不与
上(不与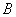 、
、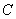 重合)的一个动点.过点
重合)的一个动点.过点 作直线
作直线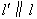 ,交抛物线于点
,交抛物线于点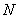 ,连结
,连结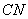 、
、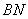 ,设点
,设点 的横坐标为.当t为何值时,
的横坐标为.当t为何值时,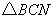 的面积最大?最大面积为多少?
的面积最大?最大面积为多少?
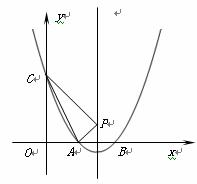

解:(1)∵抛物线 过点
过点 . ∴
. ∴
又∵ ∴
∴ ,即
,即
又∵点A在抛物线 上.
上.
∴0=12+b×1+2,b=-3
∴抛物线的解析式为:
(2)过点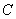 作对称轴的垂线,垂足为
作对称轴的垂线,垂足为 ,
,
∴ .
.
∴
∵ ∴
∴
∴ ,即
,即 ,
,
解得 或
或 ∴点
∴点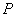 的坐标为(
的坐标为( ,
, )或(
)或( ,
, ).
).
(备注:可以用勾股定理或相似解答)
(3)易得直线 的解析式为
的解析式为 ,
,
∵点 是直线
是直线 和线段
和线段 的交点,
的交点,
∴ 点的坐标为
点的坐标为
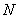 的坐标为
的坐标为
∴
∴

∴
∴当 时,
时, 最大值为1.
最大值为1.

练习册系列答案
相关题目
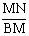 的值为( ).
的值为( ). D.
D.

 C.6 D.
C.6 D.

 0°,AD=
0°,AD= .
.
 B.
B. C.
C. D..
D..
 的值为零.
的值为零.