题目内容
9. 如图,⊙O与⊙O′交于A,B两点,AB既是⊙O的内接正六边形的一边,又是⊙O′的内接正方形的一边,且AB=12,求圆心距.
如图,⊙O与⊙O′交于A,B两点,AB既是⊙O的内接正六边形的一边,又是⊙O′的内接正方形的一边,且AB=12,求圆心距.
分析 连接OO′交AB于点C,连接OB,OA,O′A,O′B,由正多边形的性质易得△AOB和△AO′B分别是等边三角形和等腰直角三角形,再由特殊三角形的性质可求出OC和O′C的长,进而可求出OO′的长.
解答  解:连接OO′交AB于点C,连接OB,OA,O′A,O′B,
解:连接OO′交AB于点C,连接OB,OA,O′A,O′B,
∵AB既是⊙O的内接正六边形的一边,又是⊙O′的内接正方形的一边,
∴△AOB和△AO′B分别是等边三角形和等腰直角三角形,
∴OC=BC•tan∠OBC=6$\sqrt{3}$,O′C=$\frac{1}{2}$AB=6,
∴OO′=OC+O′C=6+6$\sqrt{3}$.
点评 此题考查了正多边形与圆的知识.解题的关键是熟知圆内接正六边形的边长和圆的半径相等;圆的内接正方形的对角线长为圆的直径.

练习册系列答案
相关题目
18.下列各数不属于分数的是( )
| A. | -0.314 | B. | 3.$\stackrel{•}{1}$$\stackrel{•}{4}$ | C. | 3.14… | D. | -$\frac{14}{3}$ |
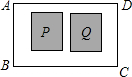 要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{4}$,求P、Q两块绿地周围的硬化路面的宽,设硬化路面的宽为x米.
要对一块长60米、宽40米的矩形荒地ABCD进行绿化和硬化,设计方案如图所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{4}$,求P、Q两块绿地周围的硬化路面的宽,设硬化路面的宽为x米.