题目内容
12.计算(1)$\sqrt{27}$-6$\sqrt{\frac{1}{3}}$$+\sqrt{48}$
(2)$\frac{2\sqrt{12}+\sqrt{3}}{\sqrt{3}}$-(1-$\sqrt{3}$)(1+$\sqrt{3}$)
分析 (1)先将式子化简,再合并同类项即可解答本题;
(2)根据二次根式的除法和平方差公式和二次根式的减法进行计算即可.
解答 解:(1)$\sqrt{27}$-6$\sqrt{\frac{1}{3}}$$+\sqrt{48}$
=$3\sqrt{3}-\sqrt{\frac{1}{3}×36}+4\sqrt{3}$
=$3\sqrt{3}-\sqrt{12}+4\sqrt{3}$
=$3\sqrt{3}-2\sqrt{3}+4\sqrt{3}$
=5$\sqrt{3}$;
(2)$\frac{2\sqrt{12}+\sqrt{3}}{\sqrt{3}}$-(1-$\sqrt{3}$)(1+$\sqrt{3}$)
=$2\sqrt{4}+1-[{1}^{2}-(\sqrt{3})^{2}]$
=4+1-(1-3)
=4+1+2
=7.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法和平方差公式.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3.若|m|=3,n2=49,且m-n>0,则m+n的值是( )
| A. | 10 | B. | 4 | C. | -10或-4 | D. | 4或-4 |
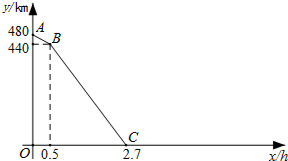 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
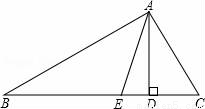
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象. 如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.
如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为135°.