题目内容
17.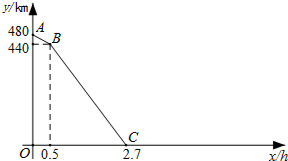 一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.(1)由图象知,慢车的速度为80km/h,快车的速度为120km/h;
(2)请在图中补全函数图象;
(3)求当x为多少时,两车之间的距离为300km.
分析 (1)根据AB段可以确定先出发的车的速度,然后根据BC段确定两车速度的和,则后出发的车的速度可以求得;
(2)根据路程是480km,则可以求得两辆车到达时的时间,然后求得各组到达的所需要的时间,再求得相距的距离即可确定;
(3)两车之间的距离是300km时有两个位置,分成相遇前和相遇后两种情况讨论即可列方程求解.
解答 解:(1)先出发的车的速度是(480-440)÷0.5=80km/h,
两车的速度的和是440÷(2.7-0.5)=200km/h,则另一辆车的速度是120km/h.
则慢车的速度是80km/h,快车120km/h.
故答案是:80,120;
(2)如下图,注意端点值.
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即(80+120)×(x-0.5)=440-300,解得x=1.2(h);(8分)
或(80+120)×(x-2.7)=300,解得x=4.2(h).(10分)故x=1.2 h或4.2 h,两车之间的距离为300km.
点评 本题考查了一次函数的图象和性质,在直角坐标系中的读图能力,搞清楚各个拐点的实际意义是关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
9.双曲线$y=\frac{k}{x}$经过点(2,3),下列各点在该双曲线上的是( )
| A. | (6,-1) | B. | (-3,2) | C. | (3,-2) | D. | (-6,-1) |
6.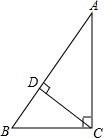 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )
如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )
如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,CD⊥AB于点D,则cot∠BCD的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{12}{5}$ | D. | $\frac{12}{13}$ |

 如图所示,两人沿着边长为90m的正方形,按A→B→C→D→A…的方向行走,甲从A点以65m/min的速度、乙从B点以75m/min的速度行走,当乙第一次追上甲时,将在正方形的AD边上.
如图所示,两人沿着边长为90m的正方形,按A→B→C→D→A…的方向行走,甲从A点以65m/min的速度、乙从B点以75m/min的速度行走,当乙第一次追上甲时,将在正方形的AD边上.