题目内容
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (n为正整数).
(n为正整数).
(1)抛物线![]() 与x轴的交点坐标为 .顶点坐标为 .
与x轴的交点坐标为 .顶点坐标为 .
(2)当n=1时,请解答下列问题:
①抛物线![]() 与x轴的交点坐标为 .顶点坐标为 .请写出抛物线y,
与x轴的交点坐标为 .顶点坐标为 .请写出抛物线y,![]() 的一条相同的性质.
的一条相同的性质.
②当直线![]() 与抛物线y,
与抛物线y,![]() ,共有4个交点时,求m的取值范围
,共有4个交点时,求m的取值范围
(3)若直线y=k(k<0)与抛物线y,![]() 共有4个交点,从左至右依次标记为点A,B,C,D,当AB=BC=CD时,求出k,n之间满足的关系式.
共有4个交点,从左至右依次标记为点A,B,C,D,当AB=BC=CD时,求出k,n之间满足的关系式.
【答案】(1)(-1,0),(3,0);(1,4) (2)①见解析 ②![]() ,且m≠
,且m≠![]() 且m≠
且m≠![]() (3)
(3)![]()
【解析】
(1)令![]() 求解即可计算与
求解即可计算与![]() 轴的交点坐标,将二次函数配方成顶点式即可求算顶点坐标;
轴的交点坐标,将二次函数配方成顶点式即可求算顶点坐标;
(2)①将![]() 代入
代入![]() 得解析式为
得解析式为![]() ,令
,令![]() 求解即可计算与
求解即可计算与![]() 轴的交点坐标,将二次函数配方成顶点式即可求算顶点坐标;根据(1)(2)点的坐标即可得出相同的性质;②分别进行考虑,当直线
轴的交点坐标,将二次函数配方成顶点式即可求算顶点坐标;根据(1)(2)点的坐标即可得出相同的性质;②分别进行考虑,当直线![]() 与抛物线y只有1个交点时联立解方程求算出
与抛物线y只有1个交点时联立解方程求算出![]() ,再考虑当直线
,再考虑当直线![]() 与抛物线
与抛物线![]() 只有1个交点时联立解方程求算出
只有1个交点时联立解方程求算出![]() ,得出结论当直线
,得出结论当直线![]() 与抛物线y,
与抛物线y,![]() ,共有4个交点时
,共有4个交点时![]() 的取值范围,同时考虑当直线
的取值范围,同时考虑当直线![]() 经过(-1,0),(3,0)时
经过(-1,0),(3,0)时![]() 的值,最终得出答案;
的值,最终得出答案;
(3)设点A,B,C,D的横坐标依次为![]() ,分别联立解方程表示出
,分别联立解方程表示出![]() ,根据题意AB=BC=CD得出
,根据题意AB=BC=CD得出![]() ,从而建立等量关系求解.
,从而建立等量关系求解.
解:(1)令![]() 即
即![]() 解得:
解得:![]()
∴与![]() 轴的交点坐标为(-1,0),(3,0);
轴的交点坐标为(-1,0),(3,0);
又∵![]()
∴顶点坐标为(1,4).
(2)当将![]() 时
时![]() ,令
,令![]() 即
即![]()
解得:![]()
∴与![]() 轴的交点坐标为(-1,0),(3,0)
轴的交点坐标为(-1,0),(3,0)
又∵![]()
∴顶点坐标为 ![]() .
.
两条抛物线的对称轴都为直线x=1,与x轴的交点坐标都为(-1,0),(3,0)等等(答案不唯一,正确即可)
②如图,当直线![]() 与抛物线y只有1个交点时,
与抛物线y只有1个交点时,

联立: ,
,
得![]()
∴![]()
∴![]()
当直线![]() 与抛物线
与抛物线![]() 只有1个交点时,
只有1个交点时,
联立:
得:![]()
∴![]()
∴![]()
∴![]()
把(-1,0)代入![]() ,得
,得![]() ,
,
把(3,0)代人![]() ,得
,得![]() ,
,
∴![]() ,且m≠
,且m≠![]() 且m≠
且m≠![]() .
.
(3)设点A,B,C,D的横坐标依次为![]() ,
,
联立:![]() ,
,
得![]()
设该方程的两个根为![]() ,
,
可得![]() .
.
联立: ,
,
得![]()
设该方程的两个根为![]() ,
,
可得![]() .
.
∵AB=BC=CD
∴![]()
∴![]()
∴![]()

【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |

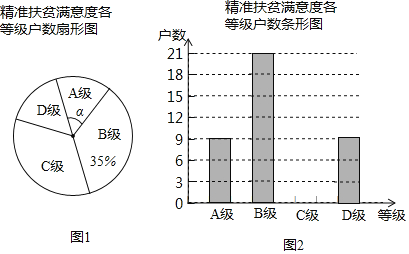
(1)表中![]() __________;
__________;![]() _________.
_________.
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)