题目内容
2.在△ABC中,∠C=90°,AB=10,AC:BC=3:4,则BC=( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即BC2+AC2=AB2,结合已知条件,即可得出BC的长.
解答 解:∵∠C=90°,AB=10,AC:BC=3:4,
∴BC2+AC2=AB2,AC:BC:AB=3:4:5,
∴BC=8;
故选:C.
点评 本题考查了勾股定理;熟记勾股定理是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
13.在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线( )
| A. | 互相垂直 | B. | 相等 | C. | 相交 | D. | 互相平行 |
10.从8:10到8:32分,时钟的分针转过的角度为( )
| A. | 122° | B. | 132° | C. | 135° | D. | 150° |
17.计算:-$\frac{5}{6}$×(-2.4)×$\frac{3}{5}$等于( )
| A. | 1.2 | B. | -1.2 | C. | 2.4 | D. | -2.4 |
7. 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )
 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )| A. | CE | B. | AD | C. | CF | D. | AB |
14.如果电影票上的“5排2号”记作(5,2),那么(4,1)表示( )
| A. | 4排5号 | B. | 5排4号 | C. | 1排4号 | D. | 4排1号 |
12.等式(1-x)( )=1-x2中,括号内应填入( )
| A. | x-1 | B. | 1-x | C. | 1+x | D. | -1-x |
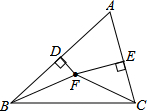 如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.
如图所示,已知在△ABC中,AB与AC的垂直平分线分别交AB于点D,交AC于点E,它们相交于点F,求证:BF=FC.