题目内容
已知关于x的函数y=(m+2)x2+2x﹣1与x轴仅有一个公共点,则m等于
﹣2或﹣3 .
考点: 抛物线与x轴的交点.
分析: 若m+2=0,一次函数与x轴只有一个交点,满足题意;若m+2≠0,根据抛物线图象与x轴只有一个交点,得到根的判别式等于0,即可求出m的值.
解答: 解:若m+2=0,一次函数y=﹣2x+1与x轴只有一个交点,满足题意,此时m=﹣2;
若m+2≠0,由二次函数y=(m+2)x2+2x﹣1图象与x轴只有一个交点,得到△=4+4m+8=0,
解得:m=﹣3,
则m=﹣2或﹣3.
故答案为:﹣2或﹣3.
点评: 此题考查了抛物线与x轴的交点,注意考虑两种情况进行分类讨论是正确解答的关键.

练习册系列答案
相关题目

 ﹣
﹣ +
+ ﹣
﹣ )×(﹣4.8)
)×(﹣4.8)
 B.
B.  C.
C.  D.
D. 

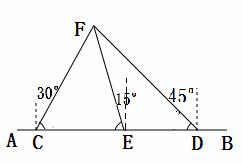
 海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.
海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.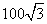 海里范围内有暗礁.若巡逻船C沿直线CF去营救船F,在去营救的途中有无触暗礁危险?(参考数据:
海里范围内有暗礁.若巡逻船C沿直线CF去营救船F,在去营救的途中有无触暗礁危险?(参考数据: ,
,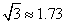 ,
, )
)
 的图象上的两点,若x1<0<x2,则y1 y2.
的图象上的两点,若x1<0<x2,则y1 y2.