题目内容
 如图,在△ABC中,AB=AC=12,DC=4,过点C作CE∥AB交BD的延长线于点E,
如图,在△ABC中,AB=AC=12,DC=4,过点C作CE∥AB交BD的延长线于点E,| AB |
| a |
| BC |
| b |
(1)求
| BE |
| a |
| b |
(2)求作向量
| 1 |
| 2 |
| BD |
| AC |
考点:*平面向量
专题:
分析:(1)由在△ABC中,AB=AC=12,DC=4,CE∥AB,可得AB=2CE,然后由
=
,
=
,即可求得
;
(2)由平行线分线段成比例定理,可得
=
,然后由三角形法则,即可求得答案.
| AB |
| a |
| BC |
| b |
| BE |
(2)由平行线分线段成比例定理,可得
| 1 |
| 2 |
| BD |
| DE |
解答:解:(1)∵CE∥AB,
∴
=
,
∵AB=AC=12,DC=4,
∴AD=8;
∴
=
=
,
∴AB=2CE,
∵
=
,
 ∴
∴
=
,
∴
=
-
=
-
;
(2)如图,
即为所求.
∵AB∥CE,
∴BD:DE=AB:CE=2,
∴
=
=
=
-
,
∵
=
+
=
+
,
∴
+
=
+
.
∴
| AD |
| DC |
| AB |
| CE |
∵AB=AC=12,DC=4,
∴AD=8;
∴
| CE |
| AB |
| 4 |
| 8 |
| 1 |
| 2 |
∴AB=2CE,
∵
| AB |
| a |
 ∴
∴| CE |
| 1 |
| 2 |
| a |
∴
| BE |
| BC |
| CE |
| b |
| 1 |
| 2 |
| a |
(2)如图,
| AF |
∵AB∥CE,
∴BD:DE=AB:CE=2,
∴
| DE |
| 1 |
| 2 |
| BD |
| 1 |
| 3 |
| BE |
| 1 |
| 3 |
| b |
| 1 |
| 6 |
| a |
∵
| AC |
| AB |
| BC |
| a |
| b |
∴
| 1 |
| 2 |
| BD |
| AC |
| 4 |
| 3 |
| b |
| 5 |
| 6 |
| a |
点评:本题考查了平面向量的知识.此题难度适中,注意掌握三角形法则的应用,注意数形结合思想的应用.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知两圆的半径分别为一元二次方程x2-7x+12=0的二根,圆心距为2,则两圆位置关系为( )
| A、外离 | B、外切 | C、相交 | D、内切 |
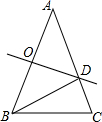 如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则∠DBC=( )
如图,在△ABC中,∠A=40°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.则∠DBC=( )| A、20° | B、25° |
| C、30° | D、80° |
若tanA的值是方程x2-(1+
)x+
=0的一个根,则锐角A=( )
| 3 |
| 3 |
| A、30°或45° |
| B、30°或60° |
| C、45°或60° |
| D、60°或90° |
 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠FED等于( )
如图,把矩形ABCD沿EF对折,若∠1=50°,则∠FED等于( )| A、50° | B、80° |
| C、65° | D、115° |
 如图,在△ABC中,DE,FG分别是边AB,AC的垂直平分线,
如图,在△ABC中,DE,FG分别是边AB,AC的垂直平分线,