题目内容
13．
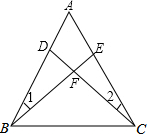如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=3．
分析 由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．
解答 解：△ABE和△ACD中，
$\left\{\begin{array}{l}{∠1=∠2}\\{∠A=∠A}\\{BE=CD}\end{array}\right.$，
∴△ABE≌△ACD（AAS），
∴AD=AE=2，AC=AB=5，
∴CE=BD=AB-AD=3，
故答案为3．
点评 本题主要考查了全等三角形的性质和判定，熟记定理是解题的关键．
练习册系列答案
相关题目
4．某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（ ）
| 劳动时间（小时） | 3 | 3.5 | 4 | 4.5 |
| 人 数 | 1 | 1 | 2 | 1 |
| A． | 中位数是4，平均数是3.75 | B． | 众数是4，平均数是3.75 | ||
| C． | 中位数是4，平均数是3.8 | D． | 众数是2，平均数是3.8 |
1．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | （-a+b）（a+b）=b2-a2 | C． | （a3）4=a7 | D． | a3+a5=a8 |
8．
如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（ ）
如图，在四边形ABCD中，AB=CD，BA和CD的延长线交于点E，若点P使得S△PAB=S△PCD，则满足此条件的点P（ ）| A． | 有且只有1个 | |
| B． | 有且只有2个 | |
| C． | 组成∠E的角平分线 | |
| D． | 组成∠E的角平分线所在的直线（E点除外） |
5．
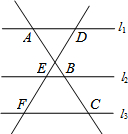如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F．已知$\frac{AB}{BC}=\frac{3}{2}$，则$\frac{DE}{DF}$的值为（ ）
如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F．已知$\frac{AB}{BC}=\frac{3}{2}$，则$\frac{DE}{DF}$的值为（ ）| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{3}{5}$ |
某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为60名．