题目内容
8. 如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB=$\frac{4}{3}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB=$\frac{4}{3}$.
分析 连接BO并延长交PA的延长线于F,连接OA,根据切线长定理得到PA=PB=2r,根据相似三角形的性质得到FB=2FA,根据勾股定理求出FB=$\frac{8}{3}$r,根据正切的概念计算得到答案.
解答 解: 连接BO并延长交PA的延长线于F,连接OA,
连接BO并延长交PA的延长线于F,连接OA,
∵PA,PB切⊙O于A、B两点,CD切⊙O于E点,
∴PA=PB,CE=CA,DE=DB,
∴PA+PB=PC+PD+CD=4r,
∴PA=PB=2r,
∵PA,PB切⊙O于A、B,
∴∠FAO=∠FBP=90°,又∠AFO=∠BFP,
∴△FAO∽△FBP,
∴$\frac{FA}{FB}$=$\frac{OA}{PB}$=$\frac{1}{2}$,
∴FB=2FA,
∴FA2+r2=(2FA-r)2,
解得,FA=$\frac{4}{3}$r,则FB=$\frac{8}{3}$r,
∴tan∠APB=$\frac{FB}{PB}$=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查的是切线长定理、锐角三角函数的概念、相似三角形的判定和性质,掌握从圆外一点作圆的切线,它们的切线长相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,所提供的信息正确的是( )
如图,所提供的信息正确的是( )
 如图,所提供的信息正确的是( )
如图,所提供的信息正确的是( )| A. | 七年级人最多 | B. | 八年级比九年级人多 | ||
| C. | 九年级女生比男生多 | D. | 九年级男生是女生两倍 |
13.“神九冲天”和“蛟龙入海”被评为2012年国内十大新闻,如果把神九的远地点330公里记作+330,则蛟龙的最大下潜深度7062米(即7.062公里)应记作( )
| A. | +7062 | B. | -7062 | C. | +7.062 | D. | -7.062 |
18.下列4对数值中是方程2x-y=1的解的是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ |
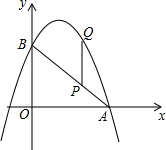 如图,抛物线y=-x2+2x+3分别与x轴正半轴、y轴交于点A,B.点P在线段AB上运动(不与点A,B重合),过点P作P作PQ∥y轴交抛物线于点Q,求PQ的最大值.
如图,抛物线y=-x2+2x+3分别与x轴正半轴、y轴交于点A,B.点P在线段AB上运动(不与点A,B重合),过点P作P作PQ∥y轴交抛物线于点Q,求PQ的最大值.