题目内容
19.用简便方法计算:(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{{9}^{2}}$)(1-$\frac{1}{1{0}^{2}}$)…(1-$\frac{1}{(n-1)^{2}}$)分析 利用平方差公式因式分解,进一步计算交错约分得出答案即可.
解答 解:原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)(1-$\frac{1}{4}$)(1+$\frac{1}{4}$)…(1-$\frac{1}{9}$)(1+$\frac{1}{9}$)(1-$\frac{1}{10}$)(1+$\frac{1}{10}$)…(1-$\frac{1}{n-1}$)(1+$\frac{1}{n-1}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{8}{9}$×$\frac{10}{9}$×$\frac{9}{10}$×$\frac{11}{10}$×…×$\frac{n-2}{n-1}$×$\frac{n}{n-1}$
=$\frac{1}{2}$×$\frac{n}{n-1}$
=$\frac{n}{2n-2}$.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
14.下列各组线段:①1cm、2cm、3cm; ②3cm、4cm、5cm;③3cm、5cm、8cm;④4cm、4cm、2cm;⑤6cm、14cm、5cm;其中能组成三角形的有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
9.下列根式中,不是最简二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
 已知∠BAC=∠C,∠BAM=∠CAN,∠AMC=∠MAN,求∠MAC的度数.
已知∠BAC=∠C,∠BAM=∠CAN,∠AMC=∠MAN,求∠MAC的度数.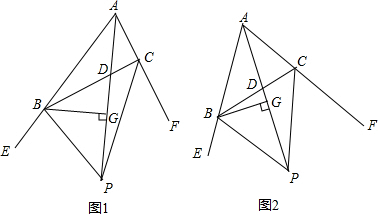
 如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB=$\frac{4}{3}$.
如图,PA,PB切⊙O于A、B两点,CD切⊙O于E点,⊙O的半径是r,△PCD周长为4r,则tan∠APB=$\frac{4}{3}$.