题目内容
 如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF.
如图,AB,CD相交于O,AC∥DB,OC=OD,AE∥BF,求证:CE=DF.考点:全等三角形的判定与性质
专题:证明题
分析:由AC与DB平行,利用两直线平行内错角相等得到两对角相等,再由OD=OC,利用AAS得到三角形BOD与三角形AOC全等,利用全等三角形对应边相等得到OA=OB,再由BF与AE平行,利用两直线平行得到两对内错角相等,利用AAS得到三角形BOF与三角形AOE全等,利用全等三角形的对应边相等即可得证.
解答:解:∵AC∥DB,
∴∠D=∠C,∠DBO=∠CAO,
在△BOD和△AOC中,
,
∴△BOD≌△AOC(AAS),
∴OB=OA,
∵AE∥BF,
∴∠BFE=∠AEF,∠FBA=∠EAO,
在△BOF和△AOE中,
,
∴△BOF≌△AOE(AAS),
∴OF=OE,
∴OD-OF=OC-OE,即DF=CE.
∴∠D=∠C,∠DBO=∠CAO,
在△BOD和△AOC中,
|
∴△BOD≌△AOC(AAS),
∴OB=OA,
∵AE∥BF,
∴∠BFE=∠AEF,∠FBA=∠EAO,
在△BOF和△AOE中,
|
∴△BOF≌△AOE(AAS),
∴OF=OE,
∴OD-OF=OC-OE,即DF=CE.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 如图所示,线段BD与线段CE相交于点A,ED∥BC,2AB=3AD,AC=8,求AE的长.
如图所示,线段BD与线段CE相交于点A,ED∥BC,2AB=3AD,AC=8,求AE的长. 如图,点M是△ABC的边BC上的一点,E、F在AM上,BE∥CF,且BE=CF,求证:S△ABM=S△ACM.
如图,点M是△ABC的边BC上的一点,E、F在AM上,BE∥CF,且BE=CF,求证:S△ABM=S△ACM.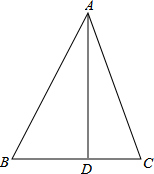 如图,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,∠BAC=45°,AD⊥BC于点D,BD=3,CD=2.
如图,在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,∠BAC=45°,AD⊥BC于点D,BD=3,CD=2.