题目内容
17．解方程：$\frac{x-4}{{x}^{2}+x-2}$=$\frac{1}{x-1}$+$\frac{x-6}{{x}^{2}-4}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：去分母得：（x-4）（x-2）=x2-4+（x-6）（x-1），
整理得：x2-6x+8=x2-4+x2-7x+6，即x2-x-2=0，
解得：x=2或x=-1，
经检验x=2是增根，分式方程的解为x=-1．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
阅读快车系列答案
相关题目
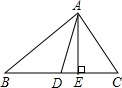如图，AD，AE分别是△ABC的中线和高，BC=6cm，AE=4cm，则△ABC的面积为12，△ABD的面积为6．
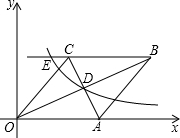如图：已知，在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=$\frac{k}{x}$（x＞0），经过D点，交BC的延长线于E点，E点的坐标是（5，8）．