题目内容
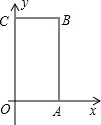
 如图,矩形OABC中,B(x,y)满足
如图,矩形OABC中,B(x,y)满足 ,点M在x轴的负半轴上,OM=2OA,P从A出发,沿射线AB方向以2单位/秒的速度运动,运动时间为t秒.
,点M在x轴的负半轴上,OM=2OA,P从A出发,沿射线AB方向以2单位/秒的速度运动,运动时间为t秒.
(1)求点M的坐标;
(2)设BP的长为y(y≠0),请用含有t的式子表示y;
(3)连接MC,CP和MP,当t为何值时,三角形CMP的面积为9?
 解:(1)∵方程组
解:(1)∵方程组 的解是
的解是 ,
,∴B点的坐标是(3,4),
∴OA=3,
∵OM=2OA,
∴OM=6,
∵点M在x轴的负半轴上,
∴点M的坐标是(-6,0);
(2)∵P从A出发,沿射线AB方向以2单位/秒的速度运动,运动时间为t秒,
∴AP=2t,
∵AB=4,
∴BP的长y=AB-AP=4-2t;
(3)∵S△CMP=S△COM+S梯形PAOC-S△AMP
=
 6×4+
6×4+ ×(2t+4)×3-
×(2t+4)×3- 2t×9
2t×9=18-6t,
∴18-6t=9,
t=
 ;
;答:当t为
 时,三角形CMP的面积为9.
时,三角形CMP的面积为9.分析:(1)先求出方程组的解,得出点B的坐标,从而得出OA的长,再求出OM的长,最后根据点M在x轴的负半轴上,即可得出点M的坐标;
(2)根据P从A出发,沿射线AB方向以2单位/秒的速度运动,运动时间为t秒,求出PA,再根据AB的长,即可得出答案;
(3)根据S△CMP=S△COM+S梯形PAOC-S△AMP,得出S△CMP=18-6t,再根据18-6t=9即可得出答案.
点评:此题考查了二元一次方程组的应用,用到的知识点是点的坐标、三角形、梯形的面积,解决问题的关键是读懂题意,找到关键描述语,列出方程组.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5). 17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为
17、如图,矩形OABC中,O是原点,OA=8,AB=6,则对角线AC和BO的交点H的坐标为

 如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )
如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )