题目内容
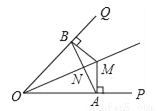
如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA.
练习册系列答案
相关题目
某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
(1)平均数为320件,中位数是210件,众数是210件;(2)不合理,定210件 【解析】试题分析:(1)根据平均数、中位数和众数的定义即可求得结果; (2)把月销售额320件与大部分员工的工资比较即可判断. (1)平均数件, ∵最中间的数据为210, ∴这组数据的中位数为210件, ∵210是这组数据中出现次数最多的数据, ∴众数为210件; (...

 ,∠BAE=100
,∠BAE=100 ,BC、DE相交于点F,则∠DFB度数是( )
,BC、DE相交于点F,则∠DFB度数是( )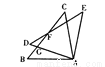
 B. 20
B. 20 C. 25
C. 25 D. 30
D. 30
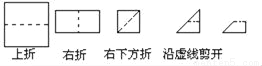
 B.
B.  C.
C.  D.
D.