题目内容
已知y=y1+y2,其中y1与x-2成正比例,y2与x成正比例,当x=0是y=5,当x=2时,y=7,求y关于x的解析式.
考点:待定系数法求一次函数解析式
专题:
分析:根据y1与x-2成正比例,y2与x成正比例,设y1=m(x-2),y2=nx,则y=m(x-2)+nx,即y=(m+n)x-2m,然后把x、y的值代入求解即可.
解答:解:∵y1与x-2成正比例,y2与x成正比例,
∴设y1=m(x-2),y2=nx,
则y=m(x-2)+nx,即y=(m+n)x-2m,
根据题意得:
,
解得:
,
则y关于x的解析式是:y=2x+5.
∴设y1=m(x-2),y2=nx,
则y=m(x-2)+nx,即y=(m+n)x-2m,
根据题意得:
|
解得:
|
则y关于x的解析式是:y=2x+5.
点评:本题主要考查了用待定系数法求函数的解析式.先根据条件列出关于字母系数的方程,解方程求解即可得到函数解析式.当已知函数解析式时,求函数中字母的值就是求关于字母系数的方程的解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列定理中有逆定理的是( )
| A、全等三角形对应角相等 |
| B、若a=0,则ab=0 |
| C、等腰三角形两腰上的高线相等 |
| D、负数的绝对值等于他的相反数 |
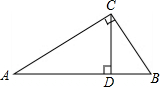 如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC.
如图,∠ACB=90°,CD⊥AB,求证:△ACD∽△CBD∽ABC. 如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.
如图,在平面直角坐标系中,已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上,并且OA、OB的长分别是方程x2-7x+12=0的两根(OA<OB),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动;同时,动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动,设点P、Q运动的时间为t秒.