Question

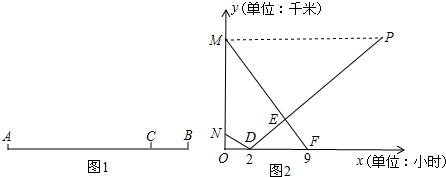
A、B两地相距630千米，客车、货车分别从A、B两地同时出发，匀速相向行驶（客车的终点站是C站，货车的终点站是A站）．客车需9小时到达C站，货车2小时可到达途中C站（如图1所示）．货车的速度是客车的 ，客车、货车到C站的距离分别为y₁、y₂（千米），它们与行驶时间x（小时）之间的函数关系（如图2所示）．

（1）客车的速度是______千米/小时，货车的速度是______千米/小时；
（2）P点坐标的实际意义是______；
（3）求两小时后，货车与C站的距离y₂与行驶时间x之间的函数关系式；
（4）求客车与货车同时出发后，经过多长时间两车相距360千米？

Answer 1

【答案】分析：（1）设客车的速度为每小时x千米，则货车的速度为每小时x千米，根据客车走的路程+货车走的路程=630建立方程求出其解即可；
（2）根据货车的速度就可以求出货车走到A地的时间，就可以求出P的坐标，进而表示出P的意义；
（3）由货车的速度可以知道P的坐标，由待定系数法就可以求出DP的解析式；
（4）分两种情况：当客车与货车相遇前两车相距360千米，当客车与货车相遇后两车相距360千米，分别建立方程求出其解即可．
解答：解：（1）设客车的速度为每小时x千米，则货车的速度为每小时x千米，由题意，得
9x+x×2=630，
解得：x=60，
∴货车的速度为：60×=45千米

（2）由题意，得
货车从B地到A地需要的时间为：630÷45=14，
∴P（14，540）
∴表示货车出发后第14小时，货车到达终点站A，此时距离C站540km；

（3）P（14，540），D（2，0），设PD的解析式为y=kx+b，由图象，得
，
解得：，
∴y=45x-90（2≤x≤14）

（4）分两种情况：
相遇前，设客车与货车行驶a小时时两车相距360千米，由题意，得
60a+45a=630-360，
解得：a= 
相遇后，设客车与货车行驶b小时后两车相距360千米，由题意，得
60x+45x=630+360，
解得：b=，
答：两车同时出发小时或小时，两车相距360千米．
故答案为：60，45．
点评：本题是一道一次函数的综合试题，考查了路程=速度×时间的运用，相遇问题的运用，待定系数法求一次函数的解析式的运用，分类讨论思想的运用，解答时结合函数图象认真分析数据的变化关系是关键．