题目内容
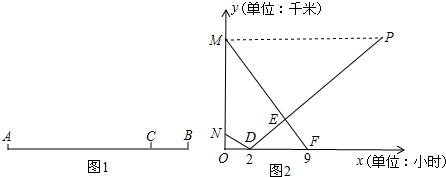
(2013•永安市质检)A、B两地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶(客车的终点站是C站,货车的终点站是A站.客车需9小时到达C站,货车2小时可到达途中C站(如图1所示).货车的速度是客车的
,客车、货车到C站的距离y(千米)与行驶时间x(小时)之间的函数关系如图2所示.
(1)客车的速度是
(2)求客车与货车出发后,经过多长时间两车相距360千米?
| 3 | 4 |
(1)客车的速度是
70
70
千米/小时,货车的速度是52.5
52.5
千米/小时;点P的坐标为(12,630)
(12,630)
.(2)求客车与货车出发后,经过多长时间两车相距360千米?

分析:(1)根据函数图象由速度=路程÷时间的数量关系就可以得出结论;
(2)设客车与货车出发后,经过x小时两车相距360千米,根据路程之间的数量关系建立方程求出其解即可.
(2)设客车与货车出发后,经过x小时两车相距360千米,根据路程之间的数量关系建立方程求出其解即可.
解答:解:(1)由函数图象,得
客车的速度为:630÷9=70千米/小时,
货车的速度为:70×
=52.5千米/小时,
货车从B到A的时间为:630÷52.5=12,
∴P(12,630);
(2)设客车与货车出发后,经过x小时两车相距360千米,由题意,得
630-(70+52.5)x=360或(70+52.5)x-630=360,
解得:x=2
或x=8
.
答:客车与货车出发后,经过2
或x=8
小时两车相距360千米.
故答案为:70,52.5,(12,630).
客车的速度为:630÷9=70千米/小时,
货车的速度为:70×
| 3 |
| 4 |
货车从B到A的时间为:630÷52.5=12,
∴P(12,630);
(2)设客车与货车出发后,经过x小时两车相距360千米,由题意,得
630-(70+52.5)x=360或(70+52.5)x-630=360,
解得:x=2
| 10 |
| 49 |
| 4 |
| 49 |
答:客车与货车出发后,经过2
| 10 |
| 49 |
| 4 |
| 49 |
故答案为:70,52.5,(12,630).
点评:本题考查了速度=路程÷时间的数量关系的运用,点的坐标的运用,列一元一次方程解行程问题的运用,解答本题时求出客车、货车的速度是关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
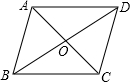 (2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是
(2013•永安市质检)如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是 (2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数
(2013•永安市质检)如图,菱形COAB的顶点B在y轴上,顶点C的坐标为(-3,2)?若反比例函数