题目内容
 如图,把一张长方形纸片沿对角线折叠,若△EDF中,∠EFD=60°,则∠BDC=
如图,把一张长方形纸片沿对角线折叠,若△EDF中,∠EFD=60°,则∠BDC=考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:根据两直线平行,同位角相等可得∠CBE=∠EFD,再根据翻折的性质求出∠CBD,然后根据直角三角形两锐角互余列式计算即可得解.
解答:解:∵矩形对边AD∥BC,
∴∠CBE=∠EFD=60°,
由翻折的性质得,∠CBD=
∠CBE=
×60°=30°,
∴∠BDC=90°-∠CBD=90°-30°=60°.
故答案为:60°.
∴∠CBE=∠EFD=60°,
由翻折的性质得,∠CBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BDC=90°-∠CBD=90°-30°=60°.
故答案为:60°.
点评:本题考查了平行线的性质,矩形的性质,翻折的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )| A、120° | B、100° |
| C、80° | D、60° |
下面判断正确的是( )
| A、一个数的相反数不是负数,这个数一定是负数 |
| B、一个数的绝对值是正数,这个数一定是正数 |
| C、两个数的和是正数,这两个数一定都是正数 |
| D、两个数的乘积为1,这两个数一定互为倒数 |
下列运算中,其结果为正数的是( )
| A、-(-2-1)2 |
| B、(-3)×(-2)2 |
| C、-32÷(-2)4 |
| D、2-3×(-2)3 |
下列说法不正确的是( )
A、
| ||||||
| B、全体实数与数轴上的点一一对应 | ||||||
C、当x<0时,
| ||||||
D、
|
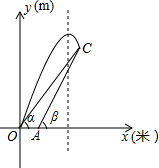 如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan
如图是某次军事演习迫击炮射击目标时在平面直角坐标系中的示意图,地面有O、A两个观测点,分别测得目标C的仰角为α、β,OA=20米,tan