题目内容
 如图,已知点F在等腰直角△ABC的斜边BC上,且有AB=BF,BD⊥AB,AF⊥DF,AD与BC交于点E,以下判断:①△ABF是等边三角形;②△BDF≌△CFA;③AE=AF.其中正确的有( )
如图,已知点F在等腰直角△ABC的斜边BC上,且有AB=BF,BD⊥AB,AF⊥DF,AD与BC交于点E,以下判断:①△ABF是等边三角形;②△BDF≌△CFA;③AE=AF.其中正确的有( )| A、②③ | B、① | C、② | D、③ |
考点:全等三角形的判定与性质,等边三角形的判定,等腰直角三角形
专题:
分析:①根据三角形的性质,大角对大边即可证得.
②根据全等三角形的判定方法AAS即可证得.
③根据等角对等边即可证得.
②根据全等三角形的判定方法AAS即可证得.
③根据等角对等边即可证得.
解答:解:①∵点F在等腰直角△ABC的斜边BC上,
∴∠AFB=∠C+∠CAF>∠C
∴AF<AB,
∴△ABF是等边三角形是错误的;
②∵AB=BF,AB=AC,
∴∠BAF=∠BFA,BF=AC
又∵∠BAC=∠AFD=90°,
∴∠BFD=∠CAF,
∵∠FBD+∠ABC=90°,∠ABC+∠C=90°,
∴∠FBD=∠C,
在△BFD与△CAF中,
,
∴△BDF≌△CFA(AAS) 正确;
③∵∠ABD=∠AFD=90°,
∴四边形ABDF共圆,
∴∠BAD=∠BFD,
∵∠AEF=∠ABC+∠BAD,∠AFE=∠ACB+∠BFD,∠ABC=∠ACB,
∴∠AEF=∠AFE,
∴AE=EF,正确;
故选A.
∴∠AFB=∠C+∠CAF>∠C
∴AF<AB,
∴△ABF是等边三角形是错误的;
②∵AB=BF,AB=AC,
∴∠BAF=∠BFA,BF=AC
又∵∠BAC=∠AFD=90°,
∴∠BFD=∠CAF,
∵∠FBD+∠ABC=90°,∠ABC+∠C=90°,
∴∠FBD=∠C,
在△BFD与△CAF中,
|
∴△BDF≌△CFA(AAS) 正确;
③∵∠ABD=∠AFD=90°,
∴四边形ABDF共圆,
∴∠BAD=∠BFD,
∵∠AEF=∠ABC+∠BAD,∠AFE=∠ACB+∠BFD,∠ABC=∠ACB,
∴∠AEF=∠AFE,
∴AE=EF,正确;
故选A.
点评:此题考查了全等三角形的判定与性质,以及等腰三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
在x轴上的点是( )
| A、(-2,3) |
| B、(-2,0) |
| C、(0,-2) |
| D、(2,-3) |
下列计算中正确的是( )
A、2
| ||||||
B、5
| ||||||
C、
| ||||||
D、3
|
如果直线y=kx+b经过一、三、四象限,那么直线y=-bx+k经过的象限为( )
| A、一、二、三象限 |
| B、一、三、四象限 |
| C、二、三、四象限 |
| D、一、二、四象限 |
在平面直角坐标系中,若M点的坐标为(-2,2),N点的坐标为(3,0),则三角形MON的面积是( )
| A、10 | B、5 | C、6 | D、3 |
 如图,菱形ABCD的边长为2,∠A=60°,点E是CD的中点,FG=1,FG两端点F,G分别在AB,AD上滑动,当AF=
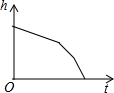
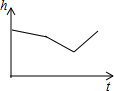
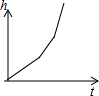
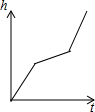
如图,菱形ABCD的边长为2,∠A=60°,点E是CD的中点,FG=1,FG两端点F,G分别在AB,AD上滑动,当AF= 匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )
匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )