题目内容
13.现定义一种新运算,对于任意有理数a、b、c、d满足$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若对于含未知数x的式子满足$|\begin{array}{l}{3}&{3}\\{2x-1}&{2x+1}\end{array}|$=3,则未知数x=-1.分析 根据已知阅读得出方程3(2x+1)-2(2x-1)=3,再去括号、移项、系数化为1,求出方程的解即可.
解答 解:∵$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,$|\begin{array}{l}{3}&{2}\\{2x-1}&{2x+1}\end{array}|$=3,
∴3(2x+1)-2(2x-1)=3,
6x+3-4x+2=3,
2x=-2,
x=-1.
故答案为:-1.
点评 本题考查了解一元一次方程,能根据已知得出方程3(2x+1)-2(2x-1)=3也是解此题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
4. 如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
 如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
如图,将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )| A. | 65° | B. | 75° | C. | 85° | D. | 不能确定 |
1.下列调查,适合用全面调查方法的是( )
| A. | 了解一批炮弹的杀伤半径 | B. | 了解三明市每天的流动人口数 | ||
| C. | 对“神舟8号”载入飞船的零件检查 | D. | 要了解三明市居民日平均用水量 |
18.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{2a}$ | C. | $\sqrt{5{a}^{2}}$ | D. | $\sqrt{0.5}$ |
 如图,已知点C在线段AB上,点M、N分别是AC、BC的中点.
如图,已知点C在线段AB上,点M、N分别是AC、BC的中点. 在线段AB上有两点C,D且AD:BD=8:6,AC:CB=2:3,若AB=90cm
在线段AB上有两点C,D且AD:BD=8:6,AC:CB=2:3,若AB=90cm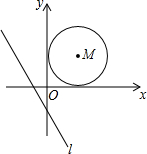 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(3,3)为圆心,3个单位长度为半径的⊙M以每秒2个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为2.5或10秒.