题目内容
7.已知二次函数y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.(1)求点A、B、C、D的坐标及对称轴方程并画出草图;
(2)当x取何值时,y>0?当x取何值时,y<0?
分析 (1)先把此二次函数化为y=(x+1)(x-3)的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=-3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;
(2)根据图象即可解答.
解答 解:(1)∵二次函数y=x2-2x-3可化为y=(x+1)(x-3),A在B的左侧,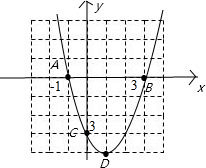
∴A(-1,0),B(3,0),
∵c=-3,
∴C(0,-3),
∵x=-$\frac{b}{2a}$=-$\frac{-2}{2}$=1,y=$\frac{4ac-{b}^{2}}{4a}$=-4,
∴D(1,-4),故此函数的大致图象为:
(2)由图象可以看出,当x<-1或x>3时,y>0;当-1<x<3时,y<0.
点评 本题考查了二次函数图象的画法及利用图象解不等式,能根据题意画出图形,再利用数形结合求解是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
17. 如图,直线a,b被直线c所截,a∥b,∠1=55°,∠BDC=30°,则∠ACD的度数为( )
如图,直线a,b被直线c所截,a∥b,∠1=55°,∠BDC=30°,则∠ACD的度数为( )
 如图,直线a,b被直线c所截,a∥b,∠1=55°,∠BDC=30°,则∠ACD的度数为( )
如图,直线a,b被直线c所截,a∥b,∠1=55°,∠BDC=30°,则∠ACD的度数为( )| A. | 45° | B. | 60° | C. | 75° | D. | 85° |
18.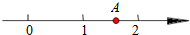 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )
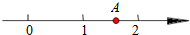 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\frac{3}{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | $\frac{3}{2}$tan45°<x<tan60° |
2.不在抛物线y=x2-2x-3上的点是( )
| A. | (-1,0) | B. | (5,12) | C. | (-4,21) | D. | (-8,-17) |
12.函数y=$\sqrt{x-5}+\sqrt{x+5}$的自变量x的取值范围是( )
| A. | x>5 | B. | x>-5 | C. | -5<x<5 | D. | x≥5 |
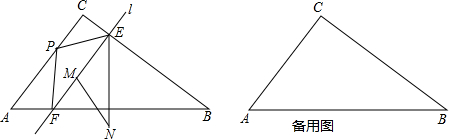
 已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF.
已知:如图,点A、E、F、C在同一直线上,∠A=∠C,AD=CB,AE=CF.