Question

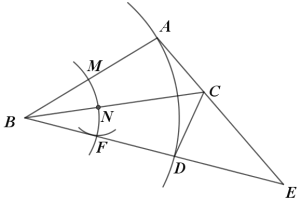
【题目】如图所示，在△ABC中，按以下步骤作图：①以点B为圆心，任意长为半径作弧，分别交BA、BC于点M、N；再以点N为圆心，MN长为半径作弧交前面的弧于点F，作射线BF交AC的延长线于点E．

②以点B为圆心，BA长为半径作弧交BE于点D，连接CD．

请你观察图形，解答下列问题：

（1）求证：△ABC≌△DBC；

（2）若∠A=100°，∠E=50°，求∠ACB的度数．

Answer 1

【答案】（1）见解析；（2）∠ACB=65°．

【解析】

（1）依据BM=BF，MN=FN，BN=BN，即可得到△BMN≌△BFN，进而得到∠ABC=∠DBC，根据SAS即可判定：△ABC≌△DBC；
（2）依据三角形内角和定理以及角平分线的定义，即可得到∠ACB的度数．

（1）如图所示，连接MN，NF，

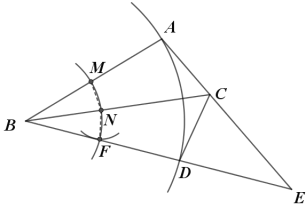
由作图可得，BM=BF，MN=FN，BN=BN，
∴△BMN≌△BFN（SSS），
∴∠ABC=∠DBC，
又∵AB=DB，BC=BC，
∴△ABC≌△DBC（SAS）；
（2）∵∠A=100°，∠E=50°，
∴∠ABE=30°，
∴∠ABC=∠ABD=15°，
∴∠ACB=180°-∠A-∠ABC=180°-100°-15°=65°．