Question

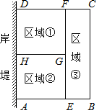
【题目】为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为米的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设的长度为米，矩形区域的面积为米．

求证：；

求与之间的函数关系式，并写出自变量的取值范围；

为何值时，有最大值？最大值是多少？

Answer 1

【答案】(1)见解析；（2）y=；（3）当时，有最大值，最大值为平方米

【解析】

（1）根据三个矩形面积相等，得到矩形AEFD面积是矩形BCFE面积的2倍，可得出AE=2BE；

（2）设BE=a，则有AE=2a，表示出a与2a，进而表示出y与x的关系式，并求出x的范围即可；

（3）利用二次函数的性质求出y的最大值，以及此时x的值即可．

解：∵三块矩形区域的面积相等，

∴矩形面积是矩形面积的倍，

又∵是公共边，

∴；

设，则，

∴，

∴，，

∴，

∵，

∴，

∴

∵，且二次项系数为，

∴当时，有最大值，最大值为平方米．