题目内容
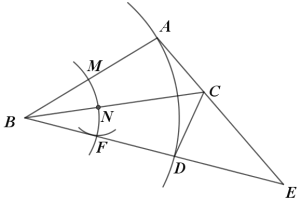
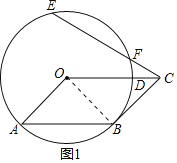
【题目】如图所示，在OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D，点E在⊙O上，连接CE与⊙O交于点F．
（1）若BC=20，求
的长度；
（2）若EF=AB，求∠OCE的度数．
【答案】（1）
的度数为
；（2）
．
【解析】
（1）连接OB，证明△AOB是等腰直角三角形，即可求解；
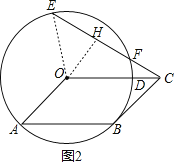
（2）连接
，过点
作
于点
，设
，根据垂径定理可表示EF即AB的长度， 再根据△AOB是等腰直角三角形，可表示OA即OE的长度，再根据勾股定理表示OH，根据OH和OC之间的关系即可求得∠OCE的度数．
（1）连接
，
是圆的切线，
．
四边形
是平行四边形，
，
．
是等腰直角三角形．
．
的度数为．
（2）连接，过点作于点，设，
，
，
四边形是平行四边形，
，
是等腰直角三角形，
，
∴
，
则
．
，
．
练习册系列答案
科学实验活动册系列答案
相关题目
