题目内容
10.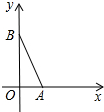 在平面直角坐标系中,点A(4,0)、B(0,8),以AB为斜边作等腰直角△ABC,则点C坐标为(6,6)和(-2,2).
在平面直角坐标系中,点A(4,0)、B(0,8),以AB为斜边作等腰直角△ABC,则点C坐标为(6,6)和(-2,2).
分析 分两种情况:(1)如图①,点C在第一象限,(2)如图②,点C在第二象限.针对每一种情况,分别画出图形,再利用全等求出距离,从而得出C点坐标.
解答 解:分两种情况: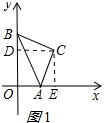
(1)如图1所示,过点C作CD⊥OB于D,CE⊥OA于E.
∵∠BCA=∠DCE=90°,
在△BCD与△ACE中,
$\left\{\begin{array}{l}{∠BDC=∠ABC}&{\;}\\{BCD=∠ACE}&{\;}\\{BC=AC}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(AAS),
∴AE=BD,CE=CD=OE,
∵AB=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴AC=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{10}$,
由勾股定理得:CE2+(CE-4)2=AC2=40,
解得:CE=:6或CE=-2(不合题意舍去).
则点C坐标为(6,6);
(2)如图2所示,过点C作CD⊥OB于D,CE⊥OA于E.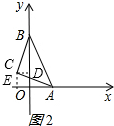
∵∠BCA=∠DCE=90°,
在△BCD与△ACE中,
$\left\{\begin{array}{l}{∠BDC=∠AEC}&{\;}\\{∠BCD=∠ACE}&{\;}\\{BC=AC}&{\;}\end{array}\right.$,
∴△BCD≌△ACE(AAS),
∴AE=BD,CE=CD=OE,
∵AB=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴AC=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{10}$,
由勾股定理得:CE2+(CE+4)2=AC2=40,
解得:CE=2,或-6(不合题意舍去).
则点C坐标为(-2,2).
综上可知点C坐标为:(6,6)和(-2,2).
故答案为:(6,6)和(-2,2).
点评 考查了坐标与图形性质、全等三角形的判定与性质、等腰直角三角形的性质;注意分类思想的运用,有一定的难度.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | ±6 | B. | ±12 | C. | ±18 | D. | ±9 |
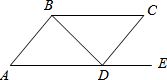 如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能使AB∥CD的是( )| A. | ∠ABD=∠CDB | B. | ∠ADB=∠CBD | C. | ∠C=∠CDE | D. | ∠C+∠ADC=180° |
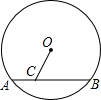 如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )
如图,⊙O的半径为5,点C在弦AB上,AC=2,BC=6,则OC的长是( )| A. | $\sqrt{13}$ | B. | 3 | C. | 4 | D. | 2$\sqrt{3}$ |
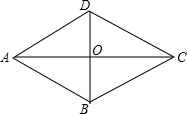 如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm.
如图,菱形ABCD的周长为48cm,它的一条对角线BD长12cm.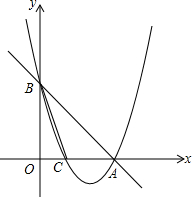 已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.
已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.