题目内容
6.在6米高的路灯下,身高1.5米的哥哥的影长为1米,身高1.2米的弟弟的影长为2米,那么哥哥和弟弟之间的距离x的取值是5米或11米.分析 根据题意画出图形,分哥哥和弟弟在路灯的同一侧与两侧进行讨论.
解答 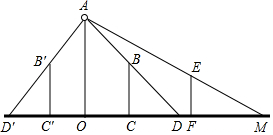 解:如图,当哥哥在BC位置时,
解:如图,当哥哥在BC位置时,
∵OA=6米,BC=1.5米,CD-1米,EF=1.2米,FM=2米,
∵BC⊥OM,
∴△BCD∽△AOD,
∴$\frac{CD}{CD+OC}$=$\frac{BC}{OA}$,即$\frac{1}{1+OC}$=$\frac{1.5}{6}$,解得OC=3米.
同理,∵△MEF∽△MAO,
∴$\frac{MF}{MF+CF+OC}$=$\frac{EF}{OA}$,即$\frac{2}{2+CF+3}$=$\frac{1.2}{6}$,解得CF=5(米),
∴此时,哥哥和弟弟之间的距离x的取值是5米;
当哥哥在B′C′的位置时,同理可得,OC′=3米,
∴C′F=3+3+5=11(米),
∴此时,哥哥和弟弟之间的距离x的取值是11米.
故答案为:5米或11米.
点评 本题考查的是相似三角形的应用,在解答此题时要注意分两种情况进行讨论.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
1.下列各式中一定是二次根式的是( )
| A. | $\root{3}{16}$ | B. | $\sqrt{a}$ | C. | $\sqrt{-{a}^{2}-1}$ | D. | $\sqrt{{a}^{2}+2}$ |
15. 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
 如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )
如图,边长为1的正方形ABCD顶点A(0,1),B(1,1);一抛物线y=ax2+bx+c过点M(-1,0)且顶点在正方形ABCD内部(包括在正方形的边上),则a的取值范围是( )| A. | -2≤a≤-1 | B. | -2≤a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{2}$ | D. | -1≤a≤-$\frac{1}{4}$ |
16.下列计算正确的是( )
| A. | $\sqrt{2}$$•\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C. | $\sqrt{8}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |