题目内容
 如图,已知等腰直角△ABC的直角边长和正方形DEFG的边长均为10厘米,BC与GF在同一直线上,开始时点B与点G重合,现在将△ABC以1厘米/秒的速度向右移动,直至点B与点F重合为止,设在移动过程中△ABC和正方形DEFG重叠部分的面积为y平方厘米,求出y(平方厘米)与x(厘米/秒)之间的函数关系式,并写出自变量的取值范围.
如图,已知等腰直角△ABC的直角边长和正方形DEFG的边长均为10厘米,BC与GF在同一直线上,开始时点B与点G重合,现在将△ABC以1厘米/秒的速度向右移动,直至点B与点F重合为止,设在移动过程中△ABC和正方形DEFG重叠部分的面积为y平方厘米,求出y(平方厘米)与x(厘米/秒)之间的函数关系式,并写出自变量的取值范围.分析:由题意可知在移动过程中△ABC和正方形DEFG重叠部分的面积为y是等腰直角三角形ABC的面积和等腰直角三角形MFC的面积差问题得解.
解答:解:∵S△ABC=
×10×10=50,
当x秒时,FC=x,
∴FM=x,
∴S△MFC=
•CF•MF=
x2,
∴在移动过程中△ABC和正方形DEFG重叠部分的面积为y=50-
x2,
∴函数关系式:y=-0.5x2+50,自变量的取值范围:0≤x≤10.
| 1 |
| 2 |
当x秒时,FC=x,
∴FM=x,
∴S△MFC=
| 1 |
| 2 |
| 1 |
| 2 |
∴在移动过程中△ABC和正方形DEFG重叠部分的面积为y=50-
| 1 |
| 2 |
∴函数关系式:y=-0.5x2+50,自变量的取值范围:0≤x≤10.
点评:本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.

练习册系列答案
相关题目
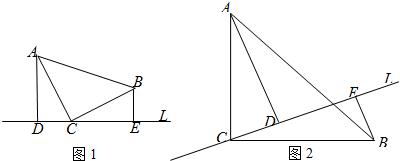
 为等腰三角形的生成三角形,简称生成三角形.
为等腰三角形的生成三角形,简称生成三角形.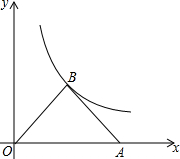 如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线
如图,已知等腰直角三角形OAB的顶点A在x轴的正半轴上,直角顶点B恰好落在双曲线 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.
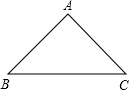
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合. 如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.
如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的边BE=DE=b,且a<b,点C、B、E放置在一条直线上,连接AD.