题目内容
8．下列各组数为三角形的三边长，其中不能组成直角三角形的是（ ）| A． | 5，7，8 | B． | 6，8，10 | C． | 5，12，13 | D． | 8，15，17 |
分析 由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
解答 解：A、∵52+72≠82，∴不能构成直角三角形；
B、∵62+82=102=100，∴能构成直角三角形；
C、∵52+122=132，∴能构成直角三角形；
D、∵82+152=172，∴能构成直角三角形．
故选A．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
相关题目
1．有下列四个论断：①-$\frac{1}{3}$是有理数；②$\frac{\sqrt{2}}{2}$是分数；③1.232232223…是无理数；④π是无理数，其中正确的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
2．如图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其最小内角为30°，则下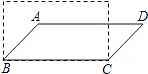
面说法正确的是（ ）
面说法正确的是（ ）| A． | 面积变为原来的一半，周长不变 | B． | 周长变为原来的一半，面积不变 | ||
| C． | 周长和面积都变为原来的一半 | D． | 周长和面积都不变 |
16．下列几何体中，不属于棱柱的是（ ）
| A． |  | B． |  | C． |  | D． |  |
3．在△ABC中，若点D、E分别在边AB、AC上，则下列条件中，一定能推出DE∥BC的是（ ）
| A． | $\frac{ED}{BC}$=$\frac{AD}{AB}$ | B． | $\frac{ED}{BC}$=$\frac{AD}{DB}$ | C． | $\frac{AD}{DB}$=$\frac{EC}{AE}$ | D． | $\frac{AD}{AE}$=$\frac{DB}{EC}$ |
13．12×$\frac{5}{6}$的结果是（ ）
| A． | 10 | B． | 4 | C． | 6 | D． | 8 |
20．如果多边形的内角和是外角和的k 倍，那么这个多边形的边数是（ ）
| A． | k | B． | 2 k+l | C． | 2 k+2 | D． | 2 k-2 |
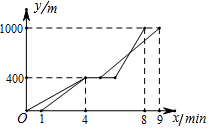甲、乙两人都从A出发经B地去C地，乙比甲晚出发1分钟，两人同时到达B地，甲在B地停留1分钟，乙在B地停留2分钟，他们行走的路程y（米）与甲行走的时间x（分钟）之间的函数关系如图所示，则下列说法中正确的个数有（ ）
18．
用不等式表示图中的解集，其中正确的是（ ）
用不等式表示图中的解集，其中正确的是（ ）| A． | x＞-3 | B． | x＜-3 | C． | x≥-3 | D． | x≤-3 |