题目内容
如图3-218(1)所示,圆内接△ABC中,AB=BC=CA,OD,OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G.
(1)求证阴影部分四边形OFCG的面积是△ABC面积的 ;
;
(2)如图3-218(2)所示,若∠DOE保持120°角度不变,求证当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的 .
.
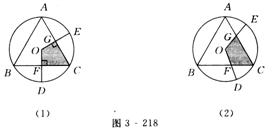
(1)证明:连接OA,OC,∵点O是等边三角形ABC的外心,Rt△OFC≌Rt△OGC≌Rt△OGA,S四边形OFCG=2S△OFC=S△OAC.∵S△OAC= S△ABC,∴S四边形OFCG=
S△ABC,∴S四边形OFCG= S
S △
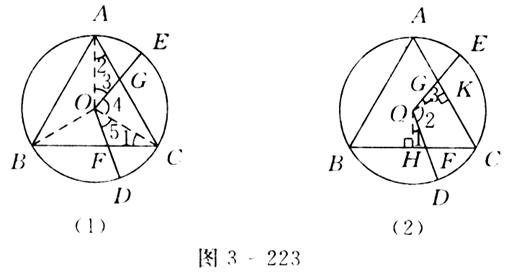
△ ABC. (2)证法1:如图3-223(1)所示,连接OA,OB和OC,则△AOC≌△COB≌△BOA,∠1=∠2.不妨设OD交BC于点F,OE交AC于点G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,
ABC. (2)证法1:如图3-223(1)所示,连接OA,OB和OC,则△AOC≌△COB≌△BOA,∠1=∠2.不妨设OD交BC于点F,OE交AC于点G,∠AOC=∠3+∠4=120°,∠DOE=∠5+∠4=120°,∴∠3=∠5.在△OAG和△OCF中,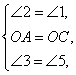 ∴△OAG≌△OCF,∴S四边形OFCG=S△AOC=
∴△OAG≌△OCF,∴S四边形OFCG=S△AOC= S△ABC.证法2:如图3-223(2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360
S△ABC.证法2:如图3-223(2)所示,不妨设OD交BC于点F,OE交AC于点G,作DH⊥BC,OK⊥AC,垂足分别为点H,K.在四边形HOKC中,∠OHC=∠OKC=90°,∠C=60°,∴∠HOK=360 °-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK=
°-90°-90°-60°=120°,即∠1+∠2=120°.又∵∠GOF=∠2+∠3=120°∴∠1=∠3.∵AC=BC,∴OH=OK.又∠OHF=∠OKG=90°.∴△OFH≌△OGK,∴S四边形OFCG=S四边形OHCK= S△ABC.
S△ABC.

练习册系列答案
相关题目
 cm,求将等腰直角三角形绕直线AC旋转一周所得旋转体的表面积
cm,求将等腰直角三角形绕直线AC旋转一周所得旋转体的表面积 .
.

 27所示,在平面直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知AO=
27所示,在平面直角坐标系中,将矩形OABC沿OB对折,使点A落在A1处,已知AO=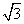 ,AB=1,则点A1的坐标是 ( )
,AB=1,则点A1的坐标是 ( )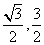 ) B.(
) B.(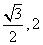 ) C.(
) C.(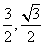 ) D.(
) D.(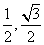 )
)
 sin 60°·
sin 60°· cos45°= .
cos45°= .