题目内容
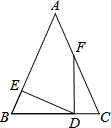 如图,已知△ABC中,点D为BC上一点,E、F两点分别在边AB、AC上,若BE=CD,BD=CF,∠B=∠C,∠A=50°,则∠EDF=
如图,已知△ABC中,点D为BC上一点,E、F两点分别在边AB、AC上,若BE=CD,BD=CF,∠B=∠C,∠A=50°,则∠EDF=考点:全等三角形的判定与性质
专题:常规题型
分析:易证△BDE≌△CFD,可得∠BDE=∠CFD,根据∠BDE+∠CDF+∠EDF=180°即可求得∠EDF的值,即可解题.
解答:解:在△BDE和△CFD中,
,
∴△BDE≌△CFD(SAS),
∴∠BDE=∠CFD,
∵∠BDE+∠CDF+∠EDF=180°,
∴∠CFD+∠CDF+∠EDF=180°,
∵∠CFD+∠CDF+∠C=180°,
∴∠EDF=∠C.
∵∠B=∠C,∠A=50°,
∴∠EDF=∠C=
(180°-50°)=65°,
故答案为65°.
|
∴△BDE≌△CFD(SAS),
∴∠BDE=∠CFD,
∵∠BDE+∠CDF+∠EDF=180°,
∴∠CFD+∠CDF+∠EDF=180°,
∵∠CFD+∠CDF+∠C=180°,
∴∠EDF=∠C.
∵∠B=∠C,∠A=50°,
∴∠EDF=∠C=
| 1 |
| 2 |
故答案为65°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△BDE≌△CFD是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
计算
(1)(-3)+(-4)-(+11)-(-9)
(2)-54×2
÷(-4
)×
(3)(
-
-
)×(-60)
(4)-12008-(-2)3-2×(-3)+|2-(-3)2|
(1)(-3)+(-4)-(+11)-(-9)
(2)-54×2
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 9 |
(3)(
| 2 |
| 3 |
| 11 |
| 12 |
| 14 |
| 15 |
(4)-12008-(-2)3-2×(-3)+|2-(-3)2|
小于
的所有正整数之和为( )
| 10 |
| A、0 | B、3 | C、5 | D、6 |
 如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD.
如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD. 如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是
如图所给的扇形的半径是12cm,周长是50cm,这个扇形的面积是