题目内容
11.若点P(m,m-4)在函数y=-$\frac{1}{2}$x+2的图象上,则点P的坐标为4.分析 直接把(m,m-4)代入函数y=-$\frac{1}{2}$x+2中可得关于m的方程,再解即可.
解答 解:∵P(m,m-4)在函数y=-$\frac{1}{2}$x+2的图象上,
∴m-4=-$\frac{1}{2}$×m+2,
m=4,
故答案为:4.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
相关题目
1. 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )
 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )| A. | 2-$\sqrt{3}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\sqrt{3}$-1 |
19.下列命题中,是假命题的是( )
| A. | 对顶角相等 | |
| B. | 同位角相等 | |
| C. | 垂线段最短 | |
| D. | 平行于同一直线的两条直线也互相平行 |
6.下列计算结果正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{3}×\sqrt{2}$=$\sqrt{6}$ | C. | 5$\sqrt{3}$-$\sqrt{3}$=5 | D. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ |
16.下列各式能运用公式法进行因式分解的有( )个
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
3.等腰三角形的两边长为3和7,则其周长为( )
| A. | 17 | B. | 13 | C. | 13或17 | D. | 以上都不对 |
 如图是由5个相同正方体组成的几何体,从左面看到的平面图形为( )
如图是由5个相同正方体组成的几何体,从左面看到的平面图形为( )



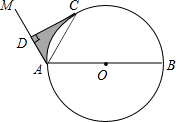 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.