题目内容
16.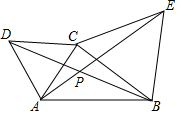 如图,点C是线段AB外一点,分别以AC、BC为边,作等边△ACD和等边△BCE,AE、BD相交于点P.
如图,点C是线段AB外一点,分别以AC、BC为边,作等边△ACD和等边△BCE,AE、BD相交于点P.(1)试说明△ACE≌△DCB的理由;
(2)求∠APB的大小.
分析 (1)根据SAS只要证明CD=CA,CB=CE,∠DCB=∠ACE,即可解决问题;
(2)设BD交AC于O.利用“8字型”证明∠APO=∠DCO即可;
解答 (1)证明:∵△ACD,△BCE都是等边三角形,
∴CD=CA,CB=CE,∠DCA=∠ECB=60°,
∴∠DCB=∠ACE,
在△ACE和△DCB中,
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$,
∴△ACE≌△DCB.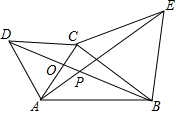
(2)解:设BD交AC于O.
∵△ACE≌△DCB,
∴∠PAO=∠ODC,
∵∠DOC=∠AOP,
∴∠APO=∠DCO=60°,
∴∠APB=180°-∠APO=120°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用“8字型”证明角相等.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
5.在△ABC和△A′B′C′中,已知∠A=∠A′,AB=A′B′,在下列说法中,错误的是( )
| A. | 如果增加条件AC=A′C′,那么△ABC≌△A′B′C′(SAS) | |
| B. | 如果增加条件BC=B′C′,那么△ABC≌△A′B′C′(SAS) | |
| C. | 如果增加条件∠B=∠B′,那么△ABC≌△A′B′C′(ASA) | |
| D. | 如果增加条件∠C=∠C′,那么△ABC≌△A′B′C′(AAS) |
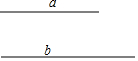 画图:已知线段a、b(不要求写画法,但要写出结论).
画图:已知线段a、b(不要求写画法,但要写出结论).