题目内容
20.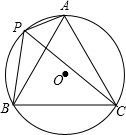 如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )
如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 由圆内接四边形的性质得到∠APB=120°,根据角平分线的性质得到∠BPC=∠APC=60°,根据圆周角定理得到∠BAC=∠ABC=60°,即可得到结论.
解答 解:∵ A、B、C、P是⊙O上的四个点,∠ACB=60°,
A、B、C、P是⊙O上的四个点,∠ACB=60°,
∴∠APB=120°,
∵PC平分∠APB,
∴∠BPC=∠APC=60°,
∵∠BPC=∠BAC,∠APC=∠ABC,
∴∠BAC=∠ABC=60°,
∵∠ACB=60°,
∴△ABC为等边三角形.
故选C.
点评 本题主要考查圆周角定理及等边三角形的判定,掌握在同圆或等圆中同弧所对的圆周角相等是解题的关键.

练习册系列答案
相关题目
15.若|x-$\frac{1}{2}$|与(y+1)2互为相反数,则x2+y3的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{3}{4}$ |
5.下列各组两项属于同类项的是( )
| A. | 3x2y和8xy2 | B. | 2m和2n | C. | x5和y5 | D. | 2与-5 |
 问题探究:观察下面由“※”组成的图案和算式,解答问题:
问题探究:观察下面由“※”组成的图案和算式,解答问题: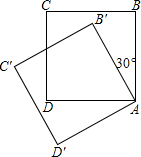 如图,把边长为4的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于$\frac{16\sqrt{3}}{3}$.
如图,把边长为4的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于$\frac{16\sqrt{3}}{3}$.