题目内容
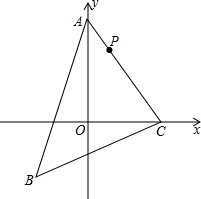 如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.
如图,已知△ABC三个顶点坐标分别为A(0,4),B(-2,-2),C(3,0),点P在线段AC上移动.当点P坐标为(1,m)时,请在y轴上找点Q,使△PQC周长最小.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:作P点关于y轴的对称点P′,连接P′C交y轴于Q,此时PQ+QC=P′C;根据两点之间线段最短,Q就是使△PQC周长最小的点;先根据待定系数法求得直线AC的解析式,进而求得P的坐标,根据轴对称的性质求得P′的坐标,然后求得直线P′C的解析式,即可求得Q的坐标.
解答: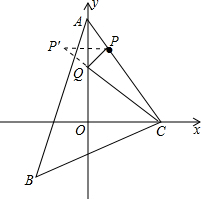 解:∵A(0,4),C(3,0),
解:∵A(0,4),C(3,0),
设直线AC的解析式为y=kx+b,
∴
,解得
,
∴直线AC的解析式为y=-
x+4;
∵点P在线段AC上移动,点P坐标为(1,m),
∴m=-
×1+4=
,
∴P(1,
),
作P点关于y轴的对称点P′,连接P′C交y轴于Q,此时PQ+QC=P′C,根据两点之间线段最短,Q就是使△PQC周长最小的点;
则P′(-1,
),
设直线P′C的解析式为y=mx+n,
∴
,解得
,
∴直线P′C的解析式为y=-
x+2,
∴Q点的坐标为(0,2).
 解:∵A(0,4),C(3,0),
解:∵A(0,4),C(3,0),设直线AC的解析式为y=kx+b,
∴
|
|
∴直线AC的解析式为y=-
| 4 |
| 3 |
∵点P在线段AC上移动,点P坐标为(1,m),
∴m=-
| 4 |
| 3 |
| 8 |
| 3 |
∴P(1,
| 8 |
| 3 |
作P点关于y轴的对称点P′,连接P′C交y轴于Q,此时PQ+QC=P′C,根据两点之间线段最短,Q就是使△PQC周长最小的点;
则P′(-1,
| 8 |
| 3 |
设直线P′C的解析式为y=mx+n,
∴
|
|
∴直线P′C的解析式为y=-
| 2 |
| 3 |
∴Q点的坐标为(0,2).
点评:本题考查了待定系数法、轴对称的性质,熟练掌握待定系数法和轴对称的性质是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列调查中,适宜采用全面调查(普查)方式的是( )
| A、某水库中鱼的种类 |
| B、某班同学立定跳远的成绩 |
| C、某型号节能灯的使用寿命 |
| D、某鞋厂生产的鞋底承受的弯折次数 |
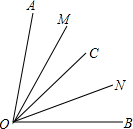 从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.
从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.
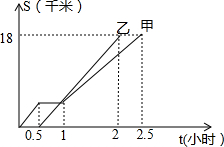 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,下列说法:
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图所示,下列说法: 一个正方体的每个面上都标注了一个汉字,如图是它的一种表面展开图,在这个正方体表面上“更”字对面上标注的汉字是( )
一个正方体的每个面上都标注了一个汉字,如图是它的一种表面展开图,在这个正方体表面上“更”字对面上标注的汉字是( )