Question

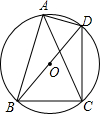如图，圆O的半径为

5

，△ABC内接于圆O，且AB=AC=4，BD为圆O的直径，求四边形ABCD的面积．

Answer 1

考点：圆周角定理,勾股定理

专题：

分析：连结AO并延长，交BC于E．先由圆周角定理得出∠BAD=∠BCD=90°，再证明AO是BC的垂直平分线，由cos∠BAO=

1 2 AB

AO

=

2

5

=

AE

AB

，求出AE=

8

5

．再根据勾股定理求得BE=CE=

4

5

，于是BC=2BE=

8

5

．再由勾股定理求得CD=

BD2-CD2

=

6

5

，AD=

BD2-AB2

=2，然后根据四边形ABCD的面积=

1

2

AB•AD+

1

2

BC•CD，代入数据即可求解．

解答：解：如图，连结AO并延长，交BC于E．
∵BD为圆O的直径，
∴∠BAD=∠BCD=90°，
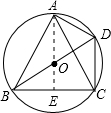∵AB=AC=4，BO=CO=R，
∴AO是BC的垂直平分线，
∵AO=BO=CO=DO=

5

，
∴cos∠BAO=

1 2 AB

AO

=

2

5

=

AE

AB

，
∴AE=

8

5

．
由勾股定理解得BE=CE=

4

5

，
∴BC=2BE=

8

5

．
由勾股定理解得CD=

BD2-CD2

=

6

5

，AD=

BD2-AB2

=2，
∴四边形ABCD的面积=

1

2

AB•AD+

1

2

BC•CD=

1

2

×4×2+

1

2

×

8

5

×

6

5

=4+

24

5

=8.8．

点评：本题考查了圆周角定理，勾股定理，难度适中．准确作出辅助线求出BC、CD、AD的长是解题的关键．