题目内容
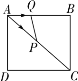
【题目】如图，已知在矩形 ABCD 中，AB＝4，AD＝3，连接 AC，动点 Q 以每秒 1 个单位的速度沿 A→B→C 向点 C 匀速运动，同时点 P 以每秒 2 个单位的速度沿 A→C→D 向点 D 匀速运动，连接 PQ，当点 P 到达终点 D 时，停止运 动，设△APQ 的面积为 S，运动时间为 t 秒，则 S 与 t 函数关系的图象大致为（ ）
A.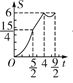
B.
C.
D.
【答案】A
【解析】
根据题意，由矩形的性质和勾股定理，得到AC=5，则得到点P的运动时间为
秒，则对运动过程进行分类讨论：①当点P从点A运动到点C的过程，即
；②点P经过点C之后，点Q到达点B时，即
；③点Q经过点B后，点P到达点D停止，即
；分别求出S与t的关系，即可得到答案.
解：由矩形的性质，得∠B=90°，AB=DC=4，AD=BC=3，
由勾股定理，得：
，
∴点P运动到点C的时间为：
秒；
点P运动到点D的时间为：
秒；
点Q运动到点B的时间为：
秒；
根据运动的情况，可分成以下三种情况：
①当点P从点A运动到点C的过程，即，
如图，作PE⊥AB于E，
∴
，
，
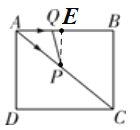
∵PE⊥AB，BC⊥AB，
∴△APE∽△ACB，
∴
，
∴
，
∴△APQ 的面积为：
（）；
②点P经过点C之后，点Q到达点B时，即；
如图，
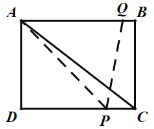
∴△APQ 的面积为：
（）；
③点Q经过点B后，点P到达点D停止，即；如图，
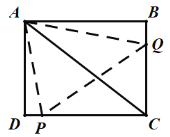
此时，
，
，
∴
，
∴△APQ 的面积为：
，
∴
（）；
∴S 与 t函数关系的图象大致为A选项中的图像；
故选：A.
练习册系列答案
相关题目
