Question

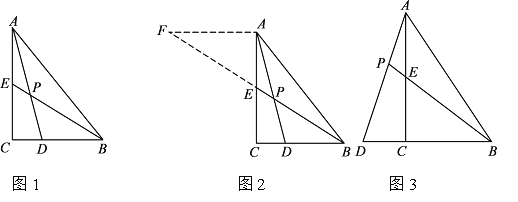
【题目】如图，在直角梯形ABCD中，AB∥CD，AD⊥AB，∠B=60°，AB=10，BC=4，点P沿线段AB从点A向点B运动，设AP=x．

（1）求AD的长；

（2）点P在运动过程中，是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似？若存在，求出x的值；若不存在，请说明理由；

（3）设△ADP与△PCB的外接圆的面积分别为S1、S2，若S=S1+S2，求S的最小值．

Answer 1

【答案】（1）2．（2）存在，2.（3）π．

【解析】

试题分析：（1）过点C作CE⊥AB于E，根据CE=BCsin∠B求出CE，再根据AD=CE即可求出AD；

（2）若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似，则△PCB必有一个角是直角．分两种情况讨论：①当∠PCB=90°时，求出AP，再根据在Rt△ADP中∠DPA=60°，得出∠DPA=∠B，从而得到△ADP∽△CPB，②当∠CPB=90°时，求出AP=3，根据且，得出△PCB与△ADP不相似．

（3）先求出S1=π，再分两种情况讨论：

①当2＜x＜10时，作BC的垂直平分线交BC于H，交AB于G；作PB的垂直平分线交PB于N，交GH于M，连结BM，在Rt△GBH中求出BG、BN、GN，在Rt△GMN中，求出MN=，在Rt△BMN中，求出BM2=，最后根据S1=πBM2代入计算即可．

②当0＜x≤2时，S2=π（），最后根据S=S1+S2=ππ即可得出S的最小值．

试题解析：（1）过点C作CE⊥AB于E，

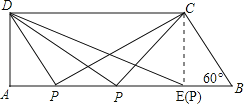
在Rt△BCE中，

∵∠B=60°，BC=4，

∴CE=BCsin∠B=4×=2，

∴AD=CE=2．

（2）存在．若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似，

则△PCB必有一个角是直角．

①当∠PCB=90°时，在Rt△PCB中，BC=4，∠B=60°，PB=8，

∴AP=AB-PB=2．

又由（1）知AD=2，在Rt△ADP中，tan∠DPA==，

∴∠DPA=60°，

∴∠DPA=∠CPB，

∴△ADP∽△CPB，

∴存在△ADP与△CPB相似，此时x=2．

②∵当∠CPB=90°时，在Rt△PCB中，∠B=60°，BC=4，

∴PB=2，PC=2，

∴AP=8．

则且，此时△PCB与△ADP不相似．1

（3）如图，因为Rt△ADP外接圆的直径为斜边PD，则S1=π（）2=π，

①当2＜x＜10时，作BC的垂直平分线交BC于H，交AB于G；

作PB的垂直平分线交PB于N，交GH于M，连结BM．则BM为△PCB外接圆的半径．

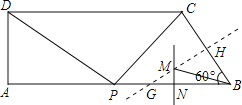
在Rt△GBH中，BH=BC=2，∠MGB=30°，

∴BG=4，

∵BN=PB=（10-x）=5-x，

∴GN=BG-BN=x-1．

在Rt△GMN中，∴MN=GNtan∠MGN=．

在Rt△BMN中，BM2=MN2+BN2=，

∴S2=πBM2=π（）．

②∵当0＜x≤2时，S2=π（）也成立，

∴S=S1+S2=π+π（）=ππ．

∴当x=时，S=S1+S2取得最小值π．