题目内容
6.计算($\frac{x+1}{{x}^{2}-x}$-$\frac{x-2}{{x}^{2}-2x+1}$)$\frac{2x-1}{x}$.分析 先把分母因式分解,再把括号内通分,接着进行同分母的减法运算,然后进行分式的乘法运算即可.
解答 解:原式=[$\frac{x+1}{x(x-1)}$-$\frac{x-2}{(x-1)^{2}}$]•$\frac{2x-1}{x}$
=$\frac{(x+1)(x-1)-x(x-2)}{x(x-1)^{2}}$•$\frac{2x-1}{x}$
=$\frac{(2x-1)^{2}}{{x}^{2}(x-1)^{2}}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的;最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式;一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.

练习册系列答案
相关题目
 如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形
如图所示,在直角坐标系xOy中,已知一次函数y=-$\frac{1}{2}$x+2的图象于x轴,y轴分别交于A,D两点,四边形ABCD是正方形 如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?
如图,有一幅长方形山水画,它的长为90cm,宽为50cm,现在需要它的四周加装一个木框,由于悬挂位置的限制,装上后整体周长不能超过320cm,那么加装的木框条的最大宽度是多少?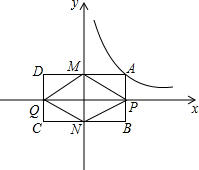 在平面直角坐标系中,一动点A在双曲线y=$\frac{12}{x}$上(x>0)移动,A点关于x、y轴的对称点分别为点B、D,B点关于y轴的对称点是点C,AB、CD分别交x轴于点P、Q,AD、BC分别交y轴于点M、N.
在平面直角坐标系中,一动点A在双曲线y=$\frac{12}{x}$上(x>0)移动,A点关于x、y轴的对称点分别为点B、D,B点关于y轴的对称点是点C,AB、CD分别交x轴于点P、Q,AD、BC分别交y轴于点M、N.