题目内容
 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )| A、AE=AC |
| B、∠B=∠D |
| C、∠BAC=∠DAE |
| D、∠C=∠E |
考点:全等三角形的判定
专题:
分析:根据∠1=∠2可利用等式的性质得到∠BAC=∠DAE,然后再根据所给的条件利用全等三角形的判定定理进行分析即可.
解答:解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
A、添加AE=AC,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意;
B、添加∠B=∠D,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意;
C、添加∠BAC=∠DAE,不能判定△ABC≌△ADE,故此选项符合题意;
D、添加∠C=∠E,可利用AAS定理判定△ABC≌△ADE,故此选项不合题意;
故选:C.
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
A、添加AE=AC,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意;
B、添加∠B=∠D,可利用SAS定理判定△ABC≌△ADE,故此选项不合题意;
C、添加∠BAC=∠DAE,不能判定△ABC≌△ADE,故此选项符合题意;
D、添加∠C=∠E,可利用AAS定理判定△ABC≌△ADE,故此选项不合题意;
故选:C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
数轴上到原点的距离等于1的点所表示的数是( )
| A、±1 | B、0 | C、1 | D、-1 |
 小明从正面观察下图所示的两个物体,看到的是( )
小明从正面观察下图所示的两个物体,看到的是( )A、 |
B、 |
C、 |
D、 |
 函数y=x+
函数y=x+| 1 |
| x |
| A、该函数的图象是中心对称图形 |
| B、y的值不可能为1 |
| C、在每个象限内,y的值随x值的增大而减小 |
| D、当x时,该函数在y时取得最小值2 |
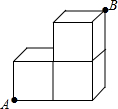 如图是由三个棱长均为1的正方体箱子堆积而成的几何体,在底端的顶点A处有一只蚂蚁,它想吃到顶端的顶点B处的食物,则它沿该几何体表面爬行的最短路程等于( )
如图是由三个棱长均为1的正方体箱子堆积而成的几何体,在底端的顶点A处有一只蚂蚁,它想吃到顶端的顶点B处的食物,则它沿该几何体表面爬行的最短路程等于( ) 小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现大树的影子恰好落在斜坡CD和地面BC上,如图所示,经测量,CD=4cm,BC=10cm,∠BCD=150°.
小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现大树的影子恰好落在斜坡CD和地面BC上,如图所示,经测量,CD=4cm,BC=10cm,∠BCD=150°. 如图所示,在等腰△ABC中,AB=AC,且△ABC的周长为22cm,过腰AB的中点D作AB的垂线,交另一腰AC于E,连接BE,若△BCE的周长是14cm,则BC=
如图所示,在等腰△ABC中,AB=AC,且△ABC的周长为22cm,过腰AB的中点D作AB的垂线,交另一腰AC于E,连接BE,若△BCE的周长是14cm,则BC=