题目内容
 如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线
如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线 的交点,则直线的解析式为________.
的交点,则直线的解析式为________.
y=-x+5
分析:根据点C的坐标确定出点A的横坐标与点B的纵坐标都是1,然后代入反比例函数解析式求出点A、B的坐标,再利用待定系数法求一次函数解析式解答.
解答:∵点C(1,1),AC∥y轴,BC∥x轴,
∴点A的横坐标是1,点B的纵坐标是1,
∴y=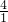 =4,
=4, =1,解得x=4,
=1,解得x=4,
∴点A、B的坐标分别为A(1,4),B(4,1),
∵A、B都在直线y=kx+b上,
∴ ,
,
解得 ,
,
∴直线的解析式为y=-x+5.
故答案为:y=-x+5.
点评:本题考查了反比例函数与一次函数的交点问题,根据点C的坐标判断出点A、B的横坐标与纵坐标,并代入反比例函数解析式求出点A、B的坐标是解题的关键,本题还考查了待定系数法求直线函数解析式,待定系数法是中学阶段常用的求函数解析式的方法,一定要熟练掌握.
分析:根据点C的坐标确定出点A的横坐标与点B的纵坐标都是1,然后代入反比例函数解析式求出点A、B的坐标,再利用待定系数法求一次函数解析式解答.
解答:∵点C(1,1),AC∥y轴,BC∥x轴,
∴点A的横坐标是1,点B的纵坐标是1,
∴y=
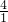 =4,
=4, =1,解得x=4,
=1,解得x=4,∴点A、B的坐标分别为A(1,4),B(4,1),
∵A、B都在直线y=kx+b上,
∴
 ,
,解得
 ,
,∴直线的解析式为y=-x+5.
故答案为:y=-x+5.
点评:本题考查了反比例函数与一次函数的交点问题,根据点C的坐标判断出点A、B的横坐标与纵坐标,并代入反比例函数解析式求出点A、B的坐标是解题的关键,本题还考查了待定系数法求直线函数解析式,待定系数法是中学阶段常用的求函数解析式的方法,一定要熟练掌握.

练习册系列答案
相关题目
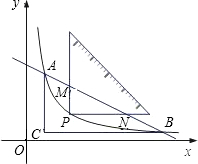 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1,| 1 |
| 2 |
| 9 |
| 2 |
| m |
| x |
A、k=-4,m=
| ||
B、k=-
| ||
| C、k=-3,m=2 | ||
| D、k=-4,m=-2 |
 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+ 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1, 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1, 如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线
如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线