题目内容
如图,将一块直角三角形纸板的直角顶点放在C(1,| 1 |
| 2 |
 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+| 9 |
| 2 |
| m |
| x |
(1)求m和k的值;
(2)设双曲线y=
| m |
| x |
| 1 |
| 2 |
分析:(1)由题意易知点A横坐标为1,代入Y=
,可用含m的代数式表示它的纵坐标;同理可表示点B坐标,再代入方程组
即可求m和k的值;
(2)用反证法证明.假设存在,运用一元二次方程判别式即可解出.
| m |
| X |
|
(2)用反证法证明.假设存在,运用一元二次方程判别式即可解出.
解答:解:(1)∵A,B在双曲线y=
(m>0)上,AC∥y轴,BC∥x轴,
∴A,B的坐标分别(1,m),(2m,
).(1分)
又点A,B在直线y=kx+
上,
∴
(2分)
解得
或
(4分)
当k=-4且m=
时,点A,B的坐标都是(1,
),不合题意,应舍去;
当k=-
且m=4时,点A,B的坐标分别为(1,4),(8,
),符合题意.
∴k=-
且m=4.(5分)
(2)假设存在点P使得MN=
AB.
∵AC∥y轴,MP∥y轴,
∴AC∥MP,
∴∠PMN=∠CAB,
∴Rt△ACB∽Rt△MPN,
∴
=
=
,(7分)
设点P坐标为P(x,
)(1<x<8),
∴M点坐标为M(x,-
x+
),
∴MP=-
x+
-
.
又∵AC=4-
=
,
∴-
x+
-
=
,即2x2-11x+16=0(※)(9分)
∵△=(-11)2-4×2×16=-7<0.
∴方程(※)无实数根.
∴不存在点P使得MN=
AB.(10分)
| m |
| x |
∴A,B的坐标分别(1,m),(2m,
| 1 |
| 2 |
又点A,B在直线y=kx+
| 9 |
| 2 |
∴
|
解得
|
|
当k=-4且m=
| 1 |
| 2 |
| 1 |
| 2 |
当k=-
| 1 |
| 2 |
| 1 |
| 2 |
∴k=-
| 1 |
| 2 |
且m=4.(5分)
(2)假设存在点P使得MN=
| 1 |
| 2 |
∵AC∥y轴,MP∥y轴,
∴AC∥MP,
∴∠PMN=∠CAB,
∴Rt△ACB∽Rt△MPN,
∴
| MP |
| AC |
| MN |
| AB |
| 1 |
| 2 |
设点P坐标为P(x,
| 4 |
| x |
∴M点坐标为M(x,-
| 1 |
| 2 |
| 9 |
| 2 |
∴MP=-
| 1 |
| 2 |
| 9 |
| 2 |
| 4 |
| x |
又∵AC=4-
| 1 |
| 2 |
| 7 |
| 2 |
∴-
| 1 |
| 2 |
| 9 |
| 2 |
| 4 |
| x |
| 7 |
| 4 |
∵△=(-11)2-4×2×16=-7<0.
∴方程(※)无实数根.
∴不存在点P使得MN=
| 1 |
| 2 |
点评:此题难度中等,考查反比例函数的性质及坐标意义.解答此题时同学们要注意运用数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
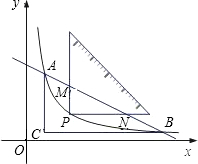 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1,| 1 |
| 2 |
| 9 |
| 2 |
| m |
| x |
A、k=-4,m=
| ||
B、k=-
| ||
| C、k=-3,m=2 | ||
| D、k=-4,m=-2 |
 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1, 如图,将一块直角三角形纸板的直角顶点放在C(1,
如图,将一块直角三角形纸板的直角顶点放在C(1, 如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线
如图,将一块直角三角形纸板的直角顶点放在点C(1,1)处,两直角边分别与x、y轴平行,纸板的另两个顶点A、B恰好为直线y=kx+b与双曲线