题目内容
定理:若x1、x2是关于x的一元二次方程x2+mx+n=0的两实根,则有x1+x2=-m,x1x2=n.请用这一定理解决问题:已知x1、x2是关于x的一元二次方程x2-2(k+1)x+k2+2=0的两实根,且(x1+1)(x2+1)=9,求k的值.
考点:根与系数的关系
专题:计算题
分析:根据判别式的意义得到△=4(k+1)2-4(k2+2)≥0,解得k≥
,再根据根与系数的关系由(x1+1)(x2+1)=9得到2(k+1)+k2+2+1=9,然后解此方程求出满足条件的k的值.
| 1 |
| 2 |
解答:解:根据题意得△=4(k+1)2-4(k2+2)≥0,
解得k≥
,
∵x1+x2=2(k+1),x1•x2=k2+2,
而(x1+1)(x2+1)=9,即x1+x2+x1•x2+1=9,
∴2(k+1)+k2+2+1=9,
整理得k2+2k-4=0,解得k1=
-1,k2=-
-1,
而∴k=
-1.
解得k≥
| 1 |
| 2 |
∵x1+x2=2(k+1),x1•x2=k2+2,
而(x1+1)(x2+1)=9,即x1+x2+x1•x2+1=9,
∴2(k+1)+k2+2+1=9,
整理得k2+2k-4=0,解得k1=
| 5 |
| 5 |
而∴k=
| 5 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程的根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.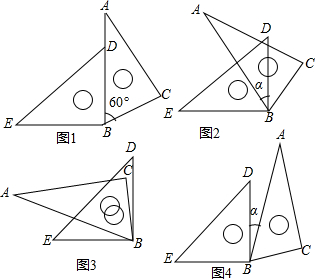 如图1是一副三角尺拼成的图案,三角尺的3个角的顶点是A、C、B,记作“三角尺ACB”;三角尺的3个角的顶点是E、B、D,记作“三角尺EBD”,且∠ACB=∠EBD=90°,∠A=30°,∠ABC=60°,∠E=∠EDB=45°.
如图1是一副三角尺拼成的图案,三角尺的3个角的顶点是A、C、B,记作“三角尺ACB”;三角尺的3个角的顶点是E、B、D,记作“三角尺EBD”,且∠ACB=∠EBD=90°,∠A=30°,∠ABC=60°,∠E=∠EDB=45°.