题目内容
 如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.
如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线.已知∠BAC=82°,∠C=40°,求∠DAE的大小.考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:先根据三角形内角和定理计算出∠B=180°-∠BAC-∠C=58°,再利用角平分线的定义得到∠BAE=
∠BAC=41°,由AD是△ABC的高得到∠ADB=90°,利用互余得∠BAD=90°-∠B=32°,然后根据∠DAE=∠BAE-∠BAD求解.
| 1 |
| 2 |
解答:解:∵∠BAC=82°,∠C=40°,
∴∠B=180°-∠BAC-∠C=58°,
∵AE是△ABC的角平分线,
∴∠BAE=∠CAE=
∠BAC=41°,
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=90°-∠B=90°-58°=32°,
∴∠DAE=∠BAE-∠BAD=41°-32°=9°.
∴∠B=180°-∠BAC-∠C=58°,
∵AE是△ABC的角平分线,
∴∠BAE=∠CAE=
| 1 |
| 2 |
∵AD是△ABC的高,
∴∠ADB=90°,
∴∠BAD=90°-∠B=90°-58°=32°,
∴∠DAE=∠BAE-∠BAD=41°-32°=9°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
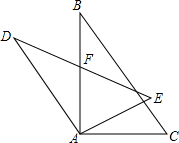 如图,三角形ADE是三角形ABC饶点A逆时针旋转30°后所得的图形,若∠D=28°,∠C=52°,AB与DE交于点F.求:∠BAE,∠BFE.
如图,三角形ADE是三角形ABC饶点A逆时针旋转30°后所得的图形,若∠D=28°,∠C=52°,AB与DE交于点F.求:∠BAE,∠BFE.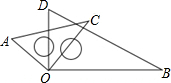 如图,将两块三角板的顶点重合.
如图,将两块三角板的顶点重合. 如图,点O是直线AB上的一点,OC⊥OD,∠AOD-∠BOC=10°,则∠BOC=
如图,点O是直线AB上的一点,OC⊥OD,∠AOD-∠BOC=10°,则∠BOC=